A Deep Learning Enhanced CT Reconstruction Algorithm for Multiphase Flow Measurement
-
摘要:
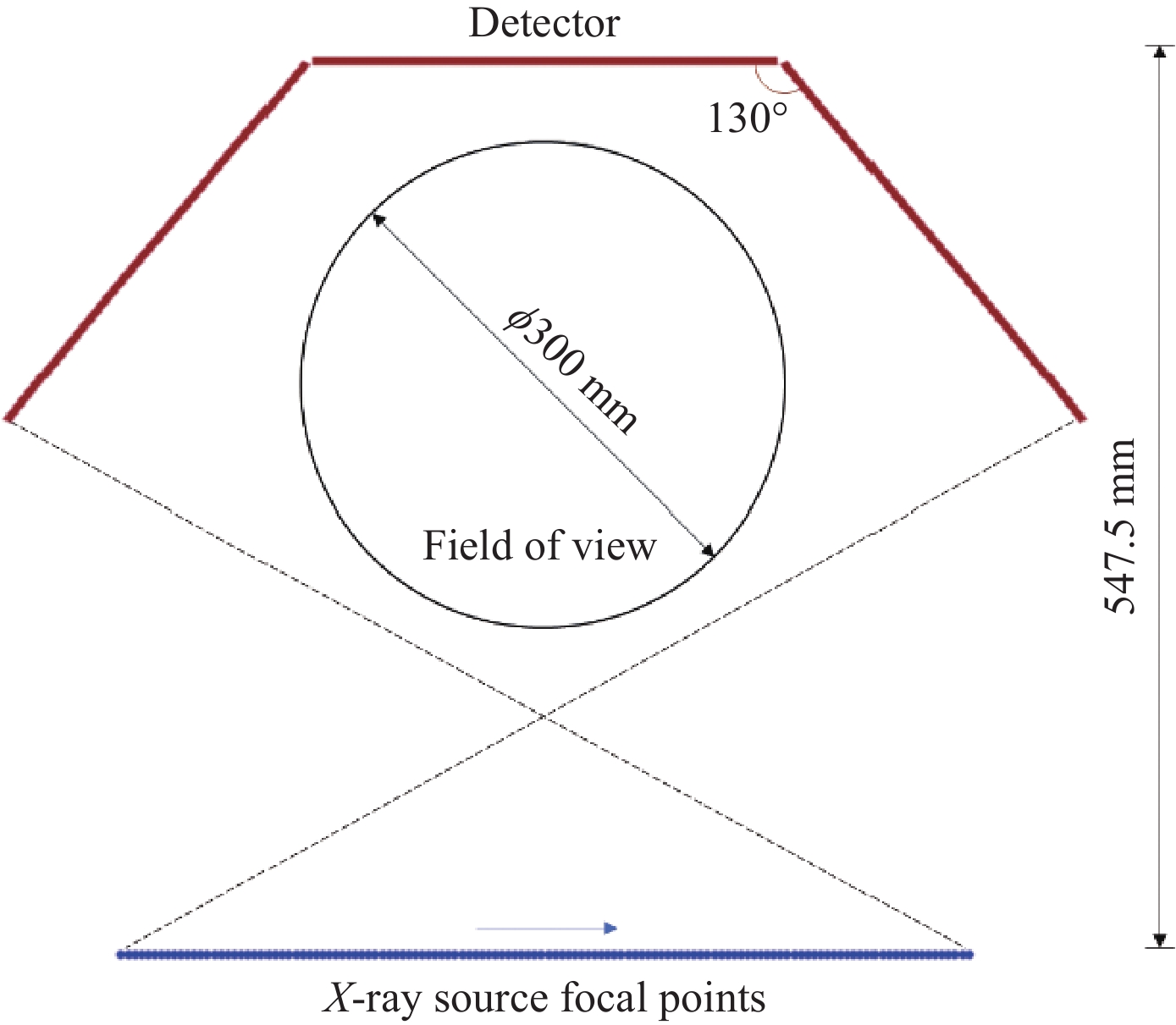
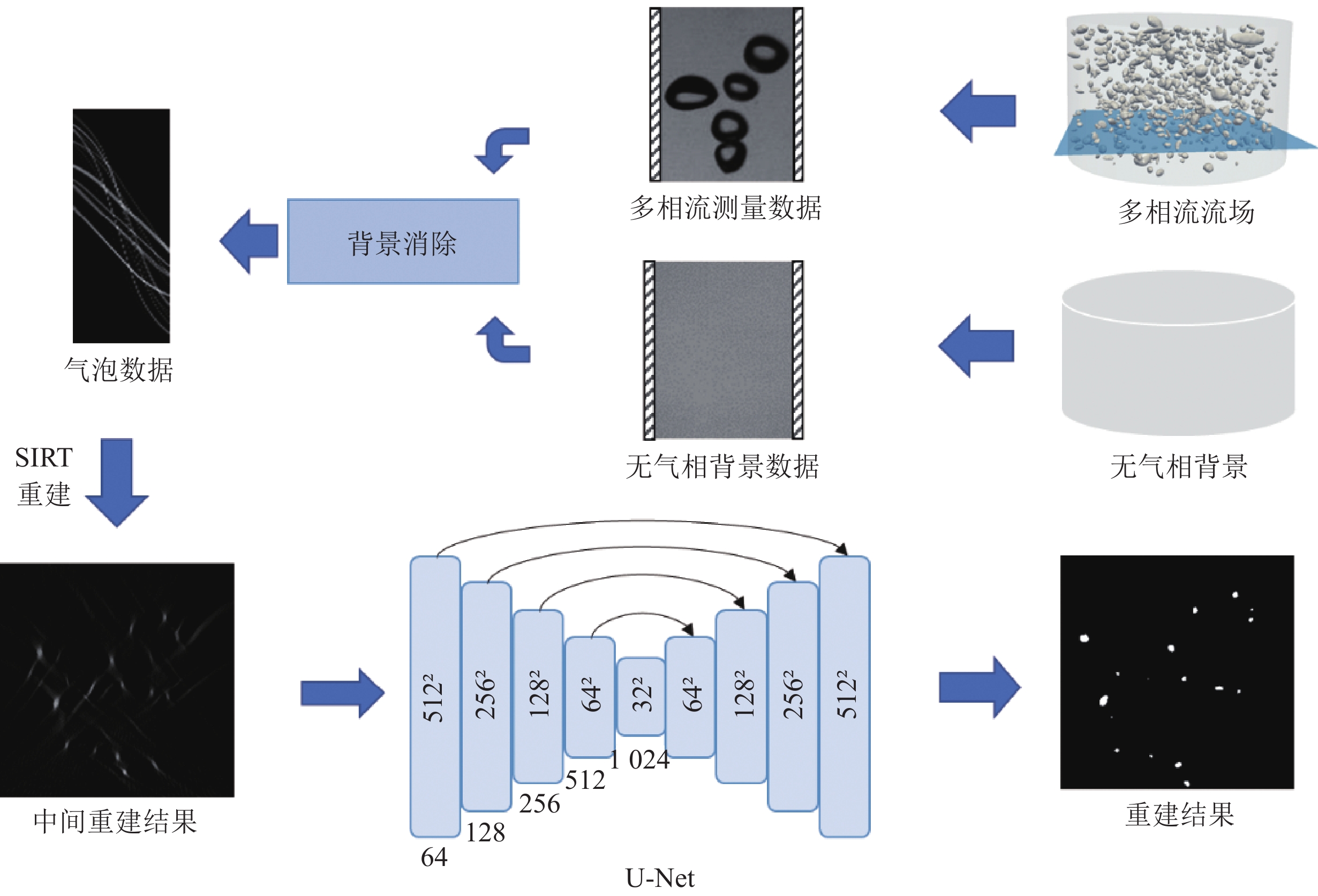
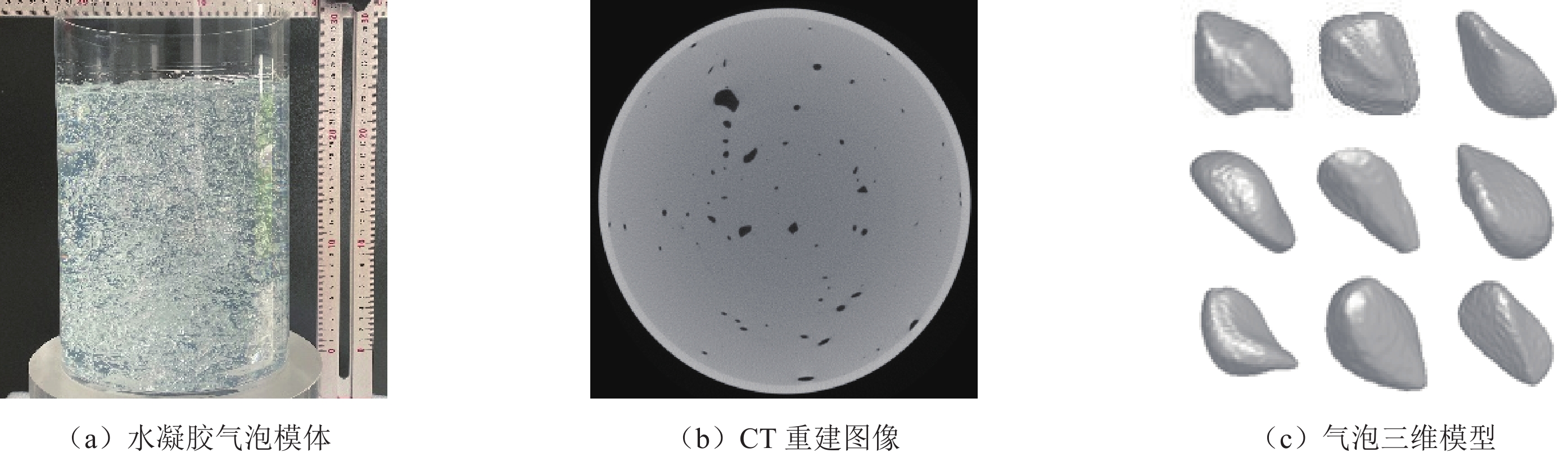
由于时空分辨率的限制，现有多相流测量技术在对流场介尺度动态结构测量时面临挑战。动态X射线CT作为一种非侵入性的检测技术，是有潜力的多相流动态结构测量方法。本研究聚焦多相流中的气液两相流体系，针对动态结构测量成像时的有限角伪影问题和重建时长问题，设计针对动态气泡结构测量的U-Net增强SIRT重建方法；基于有限角动态X射线CT系统——流场动态测量系统的硬件设计，通过收集水凝胶模体的气泡数据，建立模拟气液两相流数据集，并利用该数据集对深度学习模型进行训练，训练集效果良好。在测试集上对上述方法进行的验证显示，该方法在保证重建质量的同时显著缩短了重建时间。取得较好的效果，为解决多相流动态结构的高时空分辨性测量问题提供了一种新的技术途径。
Abstract:Measurement of multiphase flow faces critical challenges in capturing mesoscale dynamic structures due to the limitation from spatial and temporal resolution of current measuring techniques. Dynamic X-ray computed tomography (CT), as a non-invasive multiphase flow measurement technique, is promising for measuring the mesoscale structures of multiphase flow. Focusing on the gas-liquid two-phase flow in multiphase flow, this paper addresses limited angle artifacts and excessive reconstruction time in mesoscale dynamic structures, and designs a U-Net enhanced SIRT reconstruction algorithm for bubble structure measurement of gas-liquid two-phase flow. Based on the hardware designing of Flowfield Dynamic Measurement System (FDMS), a limited-angle dynamic X-ray CT system, a simulated gas-liquid two-phase flow dataset for training the deep learning model is constructed from 3D bubble structures collected from hydrogel phantoms. The proposed method achieved good results in the training and testing of the constructed dataset and significantly reduced the reconstruction time, providing a new technical approach for the efficient measurement of multiphase flow mesoscale structures.
-
Keywords:
- Multiphase flow measurement /
- Reconstruction algorithm /
- Limited-angle /
- Dynamic CT /
- Deep learning
-
双能量CT（dual-energy computed tomography, DECT）作为一种较为先进的成像技术，已广泛应用于临床实践。DECT利用物质在不同X射线能量下的衰减特性，获取高能量和低能量图像数据，从而实现单能量成像、物质成分分离和定量分析[1-3]。
在物质的定量分析中，电子密度（electron density, ED）ρe和有效原子序数（effective atomic number, EAN）Zeff不仅用于结石成分分类和肿瘤良恶性鉴别，还被用于放射治疗的蒙特卡洛剂量估算和放疗后放射性肺炎的分级评估[4-9]。因此，准确测量ρe和Zeff是实现精准影像诊断和精确剂量估算的基础。虽然已有一些研究探讨了在DECT中测量ρe和Zeff的准确性，但由于使用的CT机型（双能量成像模式）、扫描和重建参数等存在差异，导致这些研究结果难以进行比较。
本文综述近年来相关的文献研究，分析影响ρe和Zeff测量准确性的关键因素，探讨提高这些参数测量精度的方法，旨在提高影像诊断和治疗的精确性。
1. ρe和Zeff的影响因素
常规CT图像的生成是基于不同物质对X射线的衰减程度的差异，这些差异通常用衰减系数μ来量化，并以Hounsfield单位（HU）表示。因此在临床实践中，组织的HU值可能会因光子能量和扫描参数的变化而发生改变。此外，不同的组织也会表现出相同的HU值，这种现象源于衰减系数μ不仅受到光子能量的影响，还与组织密度和元素组成密切相关。1976年，Rutherford 等[10]提出利用不同能量的X射线对同一解剖结构进行至少两次扫描，以获取不同能量下的图像，进而推导出衰减系数μ与ρe和Zeff之间的关系。
目前，双能量成像作为主流的能谱CT技术，其X射线能量的解析方法会间接影响ρe和Zeff的计算结果。能量解析主要有两种方法：基于投影数据域的解析和基于图像域的解析[11]。前者通过减少射线束硬化效应，提高了解析的准确性，但计算过程更为复杂且对噪声更加敏感；后者则在计算简便性和对噪声的抗干扰能力上具有优势[12]。总之，射线束硬化效应和噪声都可能对物质的衰减系数μ造成干扰，进而影响对组织ρe和Zeff的测量精度。
1.1 射线束硬化效应的影响
CT系统采用多色能谱X射线技术，在X射线穿透介质的过程中，大量低能X射线被吸收衰减，而高能X射线的衰减相对较少，导致透射线束中的高能X射线比例提高，出现“射线束硬化”的现象[13]。在这过程中，衰减系数μ发生了变化。然而，在图像重建过程中，通常假设X射线能谱为单色，即认为衰减系数μ是恒定不变的。这种假设会导致实际的衰减系数μ与假定值之间出现偏差，进而影响到ρe和Zeff的测量精度。
随着被测物体体积的增大，射线束硬化效应变得更加显著，这将导致ρe和Zeff的测量误差进一步增大。Schaeffer等[14]在研究中指出，在较小尺寸的头部模型中，ρe和Zeff的测量值比在较大尺寸的体部模型中更为精确。然而，Almeida等[15]的研究结果与之不同，在两种不同尺寸的模型中，ρe和Zeff的测量值并无显著差异，这可能源于事先使用模体进行了ρe和Zeff的校准，有效地校正了射线束硬化效应。值得注意的是，尽管Hua等[16]没有使用模体进行校准，但他们的研究结果与Almeida等[15]相似，发现两种尺寸模型中ρe和Zeff的测量值差异控制在0.7％ 和2％ 以内。这可能与他们使用的双层探测器CT技术有关，该技术能够实现基于投影数据的材料分解，有效减轻射线束硬化的影响。
除体型尺寸外，扫描中心的偏移也是影响射线束硬化效应的一个重要因素。Schaeffer等[14]发现，当模体在上下左右4个方向上发生偏移时，Zeff会有 3％ 的变化，而ρe则相对不敏感。尽管Zeff的变化幅度不大，但这足以对物质的鉴别造成影响。例如，在偏离等中心点的模体中，血液等效组织插件（40 HU）的Zeff与未发生偏移模体中的水等效组织插件的Zeff相近。由于扫描位置受到受检者特异性及摆位技师判断偏倚的影响，难以通过其他方法进行校正，因此，制定标准化的摆位流程对于提高ρe和Zeff测量的准确性至关重要。
1.2 噪声的影响
噪声具有随机性、不确定性，会干扰正常信号的接收与处理。在CT成像领域，噪声的存在不仅影响图像的纹理，还会导致衰减系数μ的测量值与其真实值之间存在偏差。在临床实践中，降低噪声对于提升CT图像质量至关重要。为了减少噪声对衰减系数μ测量的影响，提高ρe和Zeff的测量精度，选择恰当的扫描参数和应用高效的噪声抑制技术显得尤为关键。
CT噪声主要与探测器接收的X射线光子量有关，增加X射线能量或扫描剂量可以降低噪声水平。Landry等[17]的研究表明，随着曝光剂量的增加，模体中脂肪、水、肌肉等效组织插件的ρe和Zeff的区分度提高，同时在近距离放疗的蒙特卡洛模拟中，剂量计算的误差也相应减小。然而，Hua等[16]的研究发现，在不同的管电压和剂量水平下，ρe和Zeff的测量展现出较高的准确性和稳定性。这一结果可能与Hua等[16]使用的曝光剂量范围较窄，而Landry等[17]则采用了0.5至4倍的剂量范围有关。
除了剂量和能量外，迭代算法也是影响CT噪声的关键因素。与传统的滤波反投影（filtered back projection，FBP）算法相比，迭代重建算法有效地降低了图像噪声并提高了图像质量[18-20]。Landry等[17]发现正弦图确定迭代重建（sinogram-affirmed iterative reconstruction，SAFIRE）算法在降低ρe和Zeff的标准偏差方面表现优于FBP算法，尤其在使用最大强度时。也有其他研究指出，ρe和Zeff的测量精度与迭代重建算法的强度并无明显关联[16,21]，这可能与不同研究中使用的CT机品牌和型号有关。
除了上述参数，层厚、螺距、旋转时间、卷积核等其他扫描参数同样对CT噪声有着显著影响，这些因素对ρe和Zeff测量准确性的影响值得进一步研究和探讨。
2. 不同双能量成像模式CT对ρe和Zeff的测量研究
根据不同的双能量实现方式，DECT可分为单源瞬时管电压切换模式、单源序列扫描模式、双源双能量扫描模式、单源双光束模式和单源双层探测器模式[22]（图1）。DECT通过获取物质在两种不同能量下的X射线衰减信息，利用物质在不同能量下的衰减差异进行物质分解和定量分析（图2和图3）。
![]()
![]()
图 3 电子密度和有效原子序数在胆脂瘤患者中的应用注：女，61岁，胆脂瘤伴肉芽肿。Figure 3. Application of electron density and effective atomic number in patients with cholesteatoma.（1）单源瞬时管电压切换模式DECT可在机架旋转期间实现高低电压的快速切换，尽管X射线投影角度几乎相同，允许基于投影数据域进行能量解析，但由于时间分辨力的损失，会在一定程度上影响能量解析的准确性。
当前的研究在评估Zeff测量的准确性方面展现了不同结果[21,24,25]。例如，Goodsitt等[24]通过模体实验得出Zeff的测量相对误差控制在15％ 以内的结论。相对地，Kawahara等[25]报告称Zeff的测量相对误差在5.1％ 以内。这种差异可能是因为各研究中所采用的CT机型和扫描参数不同，以及模体材料和结构的多样性所致。在ρe测量的准确性方面，Ogata等[26]发现在不同单能级图像中，模体所有材料的ρe测量相对误差控制在1.1％ 以内。目前，基于单源瞬时管电压切换模式的DECT测量ρe准确性的研究相对较少，未来可进一步探索。
（2）单源序列扫描模式DECT分别以高、低能量进行两次扫描实现双能量成像。两套独立的高低能量图像具有完全的能量分离效果，这种特性有助于提高ρe和Zeff的测量准确性。当前，相关研究表明ρe和Zeff的测定具有较高的精度，有助于提高放射治疗计划的准确性[14,27-29]。其中Schaeffer等[14]基于模体实验发现Zeff的测量相对误差为3.2％，并且认为与Kawahara等[25]基于单源瞬时管电压切换模式 DECT的研究结果相似（Zeff的测量相对误差为2.5％）。
在单源序列扫描成像模式下，两次球管旋转扫描之间存在一定的时间（如某品牌CT高低管电压扫描间隔为180～800 ms[28]），可能会影响空间配准效果，并且在临床实践中由于受到受检者运动的影响，导致材料分解存在偏差[30]。此外，较大的能谱分离效果有助于产生更好的材料区分效果，提高ρe和Zeff的准确性。目前单源序列扫描模式DECT的高能量成像多采用135 kVp的管电压，能谱分离效果略低于单源瞬时管电压切换模式DECT的140 kVp[25]。
（3）双源双能量扫描模式DECT具有较大的能谱分离优势，它采用两套X射线球管和探测器，对同一解剖平面分别发射高、低管电压的X射线并由相应的探测器采集数据。
随着技术的进步，目前双源DECT多采用能谱纯化技术进一步增大能谱分离效果，减少射线束硬化伪影，提高了ρe和Zeff的测量准确性[15,31-32]。然而，两套探测器的空间位置设计也会对ρe和Zeff的测量带来一定的影响，仅35.5 cm的全扫描视野，对于超力型成年受检者的ρe和Zeff的测量具有局限性。此外，鉴于高、低能量数据采集的相位差异，该双能量CT采用了一种对噪声反应更为敏感的图像域能量解析技术。然而，当两套探测器同时捕获高能和低能X射线时，交叉散射的产生是不可避免的，这种散射会加剧噪声，从而可能对ρe和Zeff的精确测量带来不利影响。
（4）单源双光束模式DECT采用分离滤波技术，使X射线束预先分离成高、低能量的两种光子束，由对应位置的探测器沿Z轴方向分别接收，使得同一解剖区域接收高、低能两种X射线束存在时间差异，同样地基于图像域进行能量解析。尽管该模式DECT在成像过程中也容易受到光子交叉、散射等影响，但是相关研究发现单源双光束模式DECT在测量ρe和Zeff的准确性方面劣于双源DECT[15]。该研究发现第2代、第3代双源DECT的ρe和Zeff的测量相对误差分别在1.2％ 和6.2％ 以内，然而单源双光束DECT的ρe和Zeff的测量相对误差最大可达15.3％ 和28.1％。较大的测量误差可能源于单源双光束DECT的高能和低能数据均源自相同的管电压设置，这种设计导致能谱分离效果相对较弱，从而使得成像系统对图像噪声和伪影更为敏感，影响了ρe和Zeff的准确性。
（5）单源双层探测器模式DECT同样对高能和低能数据采用了相同的管电压设置，并且存在使用相同管电流所致的高、低能光谱图像的噪声水平不同的局限，但相关研究显示出了稳健的ρe和Zeff的测量准确性[16,33]。
Hua等[16]基于模体实验发现ρe的测量相对误差范围在 -0.1％ 至1.1％，Zeff的测量相对误差范围为 -2.3％ 至1.7％。这些发现可以归因于该模式的DECT采用了独特的设计：一个X射线球管与空间上对称分布的上下两层探测器相结合。这种双层探测器配置能够同步捕获高、低能量的X射线信息，实现了基于投影数据域的材料分解[34]。从理论上讲，这种方法相较于基于图像域的材料分解具有一定的优势。
3. 总结与展望
DECT根据不同能量下物质衰减系数μ的差异进行物质分解，以实现单能量CT扫描无法评估的物质特性，其中ρe和Zeff在评估材料特性和放疗剂量估算中发挥着重要的作用。本文重点探讨影响ρe和Zeff测量精度的射线束硬化效应和噪声两大关键因素，并详细分析不同双能量成像模式CT对ρe和Zeff测量准确性的具体影响，明确了各成像模式的优势与局限。
鉴于此，未来的研究需进一步探索和优化算法，以减轻射线束硬化效应和噪声的不利影响，从而提升图像质量和测量的精确度。同时，由于不同双能量成像模式CT对ρe和Zeff测量准确性的差异化影响，未来的工作还需对这些成像模式进行细致的比较研究，并针对不同双能量成像模式CT，探索所使用机型的最佳成像条件以提高ρe和Zeff的测量准确性。
-
![]()
图 1 流场动态结构测量系统几何示意图
Figure 1. Geometric arrangement of Flowfield Dynamic Measurement System
![]()
图 2 U-Net强化的CT加速重建算法整体流程示意图
Figure 2. Overall procedure of dynamic CT measurement and U-Net enhanced reconstruction
![]()
图 3 基于水凝胶静态气泡模体获取气泡三维模型
Figure 3. 3D bubble models from hydrogel static bubble phantom
![]()
图 5 流场原始切片和不同重建方法的重建结果
Figure 5. Original flowfield slice and reconstruction results from different methods
![]()
图 6 U-Net增强重建结果流场的三维可视化
Figure 6. 3D Visualization of flowfield reconstructed by U-Net enhanced reconstruction method
表 1 不同重建方法的测试结果数据对比
Table 1 Analysis of testing results from different reconstruction methods
方法 SSIM 精确率/% 召回率/% 运行时间/s SIRT+二值化 0.980 71.6 46.9 0.87 TV正则化+二值化 0.372 37.3 5.8 86.43 SIRT+U-Net 0.985 86.8 71.6 0.91 
下载: 导出CSV
-
[1] GE W, CHEN F, GAO J, et al. Analytical multi-scale method for multi-phase complex systems in process engineering—Bridging reductionism and holism[J]. Chemical Engineering Science, 2007, 62(13): 3346-3377. DOI: 10.1016/j.ces.2007.02.049.
[2] MENG F. Computed tomography in process engineering[J]. Chemical Engineering Science, 2022: 117272. DOI: 10.1016/j.ces.2021.117272.
[3] FISCHER F, HAMPEL U. Ultra fast electron beam X-ray computed tomography for two-phase flow measurement[J]. Nuclear Engineering and Design, 2010, 240(9): 2254-2259. DOI: 10.1016/j.nucengdes.2009.11.016.
[4] STüRZEL T, BIEBERLE M, LAURIEN E, et al. Experimental facility for two- and three-dimensional ultrafast electron beam X-ray computed tomography[J]. Review of Scientific Instruments, 2011, 82(2): 023702. DOI: 10.1063/1.3529435.
[5] MUDDE R F. Bubbles in a fluidized bed: A fast X-ray scanner[J]. AIChE Journal, 2011, 57(10): 2684-2690. DOI: 10.1002/aic.12469.
[6] GRAAS A B M, WAGNER E C, VAN LEEUWEN T, et al. X-ray tomography for fully-3D time-resolved reconstruction of bubbling fluidized beds[J]. Powder Technology, 2024, 434: 119269. DOI: 10.1016/j.powtec.2023.119269.
[7] 唐华平, 陈志强, 何武, 等. CNT冷阴极微焦点X射线管研制[J]. 真空电子技术, 2023(6): 23-27,44. DOI: 10.16540/j.cnki.cn11-2485/tn.2023.06.04. TANG H P, CHEN Z Q, HE W, et al. Development of a Micro-focus X-Ray tube based on carbon nanotube cathode[J]. Vacuum Electronics, 2023(6): 23-27,44. DOI: 10.16540/j.cnki.cn11-2485/tn.2023.06.04.
[8] KAK A C, SLANEY M. Principles of computerized tomographic imaging[M]. Society for Industrial and Applied Mathematics, 2001. DOI: 10.1137/1.9780898719277.
[9] LEULIET T, FRIOT--GIROUX L, BAAZIZ W, et al. Efficiency of TV-regularized algorithms in computed tomography with Poisson-Gaussian noise[C]//2020 28th European Signal Processing Conference (EUSIPCO). 2021. DOI: 10.23919/eusipco47968.2020.9287762.
[10] XU J, ZHAO Y, LI H, et al. An image reconstruction model regularized by edge-preserving diffusion and smoothing for limited-angle computed tomography[J]. Inverse Problems, 2019: 085004. DOI: 10.1088/1361-6420/ab08f9.
[11] HUANG Y, WÜRFL T, BREININGER K, et al. Some investigations on robustness of deep learning in limited angle tomography[M]//Medical Image Computing and Computer Assisted Intervention–MICCAI 2018, Lecture Notes in Computer Science. 2018: 145-153. DOI: 10.1007/978-3-030-00928-1_17.
[12] TAO X, DANG Z, ZHENG Y, et al. Limited-angle artifacts removal and jitter correction in soft x-ray tomography via physical model-driven deep learning[J]. Applied Physics Letters, 2023, 123(19). DOI: 10.1063/5.0167956.
[13] 石常荣, 肖永顺, 李俊江, 等. 基于WDCT网络的混凝土CT图像增强算法[J]. CT理论与应用研究, 2021, 30(1): 1-8. DOI: 10.15953/j.1004-4140.2021.30.01.01. SHI C R, XIAO Y S, LI J J, et al. An enhancement algorithm for concrete imaging based on WDCT network[J]. CT Theory and Applications, 2021, 30(1): 1-8. DOI: 10.15953/j.1004-4140.2021.30.01.01.
[14] WURFL T, HOFFMANN M, CHRISTLEIN V, et al. Deep learning computed tomography: Learning projection-domain weights from image domain in limited angle problems[J]. IEEE Transactions on Medical Imaging, 2018: 1454-1463. DOI: 10.1109/tmi.2018.2833499.
[15] WANG J, ZENG L, WANG C, et al. ADMM-based deep reconstruction for limited-angle CT[J]. Physics in Medicine & Biology, 2019: 115011. DOI: 10.1088/1361-6560/ab1aba.
[16] 黄清萍, 金鑫, 许晓飞, 等. X射线衍射技术在安检领域的研究进展[J]. CT理论与应用研究, 2023, 32(6): 843-856. DOI: 10.15953/j.ctta.2023.158. HUANG Q P, JIN X, XU X F, et al. Research progress of X-ray diffraction technology in security inspection[J]. CT Theory and Applications, 2023, 32(6): 843-856. DOI: 10.15953/j.ctta.2023.158.
[17] RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutional networks for biomedical image segmentation[M]//Navab N, Hornegger J, Wells W M, et al. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, 9351. Cham: Springer International Publishing, 2015: 234-241. DOI: 10.1007/978-3-319-24574-4_28.
[18] van AARLE W, PALENSTIJN W J, CANT J, et al. Fast and flexible X-ray tomography using the ASTRA toolbox. [J]. Optics Express, 2016: 25129. DOI: 10.1364/oe.24.025129.
[19] WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI: 10.1109/TIP.2003.819861.
计量
- 文章访问数: 22
- HTML全文浏览量: 8
- PDF下载量: 2
