Industrial CT Image Denoising Network Based on Channel Attention Mechanism
-
摘要:
在工业CT中,使用含噪的投影数据进行重建,会导致重建图像中的噪声增加,降低重建图像的信噪比。当投影数据质量较差时,经典的降噪和重建算法无法有效的去除噪声。为了提高CT重建图像的质量,本文提出一种基于深度学习的去噪方法。该方法将通道注意力机制模块嵌入到解码器阶段,通过自适应地调整通道的权重,从而提高网络在去噪过程更好地保留图像的结构细节。实验结果表明,所提方法能够显著地去除噪声并有效保护边缘细节,且在视觉效果和定量指标结果上都要优于其他对比方法。
Abstract:In industrial computerized tomography (CT), using noisy projection data for reconstruction increases the noise in the reconstructed image and reduces the signal-to-noise ratio (SNR). When the quality of projection data is poor, classical denoising and reconstruction algorithms are ineffective in removing the noise. To improve the quality of low signal-to-noise CT reconstructed images, this study proposes a deep learning-based denoising method. The method integrates squeeze-and-excitation blocks into the decoder phase and adaptively adjusts the weights of the channels to better preserve structural details during the denoising process. Experimental results demonstrate that the proposed method significantly reduces the noise and effectively preserves edge details, outperforming other comparative methods in both visual quality and quantitative values.
-
Keywords:
- Industrial CT /
- Low SNR /
- Image denoising /
- Deep learning /
- Channel Attention Mechanism
-
慢性阻塞性肺疾病(chronic obstruction pulmonary disease,COPD)是一种以小气道病变和肺气肿为主要特征的异质性疾病,其发生率男性高于女性,目前是世界第3大死亡原因,并且发病率和死亡率一直在上升[1-3]。目前COPD诊断的最佳标准仍然是肺功能检查[4],临床上用肺功能来判断COPD严重程度,但是肺功能无法区分气流阻塞的病理类型,也无法区分肺气肿及小气道病变的贡献程度[5]。肺功能正常的吸烟者通常会被认为没有疾病,但吸烟者有呼吸道症状和急性加重病史,并且此类患者在CT上常有肺气肿和支气管壁增厚,而在此类人群中CT发现肺气肿可以预测进行性肺气肿、肺功能丧失和更高的死亡率[6],所以早期发现COPD易感人群肺气肿的分布比例对于其病情评估及预后有重要作用。
师美娟等[7]通过分析 CT双气相不同肺气肿阈值低衰减区(low attenuation area,LAA)占全肺体积百分比LAA%-950和LAA%-910可以评估不同严重程度肺气肿分布比例的不同;Galbán等[8]首次提出参数反应图(parameter response mapping,PRM)应用到CT扫描的可行性;此后研究表明双气相CT配准可以精确的区分及定量测量功能性小气道病变(fSAD)、肺气肿(Emph)和正常(Normal)区域[9];本课题组前期研究[10-12]表明胸部定量 CT能够早期、精准、客观的评估COPD严重程度,并且优于传统肺功能检查;梁志冉等[13]研究结果显示在无症状青年女性中存在少量肺气肿。因此我们推测在轻中度COPD中,肺气肿指标在判断疾病严重程度及早期诊断中具有极大临床实用价值,很有必要在COPD早期阶段筛选出最优CT定量肺气肿指标。
既往研究基本都是基于单气相CT定量指标来评估肺气肿,本研究纳入双气相CT配准新的定量指标进行评估肺气肿并与既往的指标比较。本研究纳入正常人群和轻中度COPD患者,来探讨双气相不同阈值和配准两种方法对轻中度COPD患者肺气肿的诊断效能及准确性,以筛选出最优的诊断轻中度COPD患者肺气肿的定量CT指标。
1. 资料与方法
1.1 一般资料
回顾性收集延安大学附属医院2018年6月至2021年6月进行呼、吸双相胸部CT检查的吸烟人群,其中包括52例确诊COPD患者,纳入参加体检的正常对照者(肺功能检查未达COPD诊断标准(FEV1/FVC≥0.7)55例。
纳入标准:所纳入的受试者年龄不低于40岁;双气相图像清晰完整,软件能够进行肺裂的正确分割。排除标准:年龄小于40岁或大于80岁;不能配合双气相扫描者;具有肺部手术、创伤史以及胸廓畸形等;大面积炎症、肺肿瘤、结核及大量胸腔积液患者;支气管哮喘、肺结核、支气管扩张及肺动脉高压等其他呼吸系统疾病患者;职业性粉尘接触史。
本研究通过延安大学附属医院伦理委员会批准[2018032],所有受试者知情同意并签署了知情同意书。
1.2 CT检查
所有患者在检查前均进行深吸气末与深呼气末的屏气训练,采用联影UCT-760 128层螺旋CT对入选患者分别在深吸气及深呼气末行肺尖至肺底行全肺低剂量扫描。
扫描参数:管电压120 kV,自适应动态管电流(选择剂量等级2,范围30~40 mAs,符合胸部低剂量参考推荐[14]),准直器宽度128×0.625 mm,螺距1.0875,转速0.5 s/圈,扫描层厚5 mm,双气相图像行骨算法1 mm薄层KARL迭代重建[11],视野350~450 mm,矩阵512×512。
根据剂量报告并采用成人胸部有效剂量权重因子K=0.014,得出有效辐射剂量为(3.71±0.28)mSv[10]。
1.3 图像处理及分析
原始DICOM数据导入“数字肺”测试平台进行分析,基于肺裂为片状,利用Hough变换进行分割来获得5个肺叶,计算吸气相<-950 HU像素占全肺的比值(吸气相LAA%-950)、呼气相<-910 HU像素占全肺的比值(呼气相LAA%-910)[9]。然后进行双气相图像配准,吸气和呼气图像的体积是空间上对齐到一个单一的几何框架使用一个薄板样条,以相互信息为对象函数。
每个实质体素(即图像数据集中最小的体积单位)使用肺气肿指数和空气捕捉阈值进行分类,吸气扫描时由COPDGene定义为 -950 HU,呼气扫描时为 -856 HU,并用于生成体素成对实质体素HU值的联合密度直方图。这使得每个体素被分类为正常、肺气肿或功能性小气道疾病。
通过将一个分类中的所有体素求和并归一化为总肺体积,计算出每个分类的相对体积[15]:吸气相CT值>-950 HU,呼气相CT值≤-856 HU的像素占全肺容积的百分比(the percentage of the area of functional small airway disease,PRMfSAD%)为小气道病变区,标记为黄色区;吸气相≤-950 HU,呼气相 ≤-856 HU的像素占全肺容积的百分比(the percentage of the area of emphysema,PRMEmph%)为肺气肿区,标记为红色区;吸气相>-950 HU,呼气相>-856 HU的像素占全肺容积的百分比(the percentage of the area of normal,PRMNormal%)为正常区,标记为绿色区。PRMfSAD%、PRMEmph%和PRMNormal%3种区域总和不等于100%,剩余区域不在阈值范围内,约占10%,被证实和肺功能无相关性,怀疑是噪音或是由于配准带来的误差,因而没有进行颜色编码[16](图1)。
1.4 肺功能检查
患者均需在CT检查后的3天内且情况稳定时进行肺功能(pulmonary function test,PFT)检查,分别测量:用力肺活量(FVC)、第1秒用力呼气容积占预计值的百分比(FEV1%)、FEV1占用力肺活量的百分比(FEV1/FVC)。
根据2023年慢性阻塞性肺疾病全球倡议(global initiative for chronic obstructive lung disease,GOLD)诊断标准[17]对COPD患者进行分级:GOLD 1级21例、GOLD 2级31例。
1.5 统计学分析
采用SPSS 26.0软件进行统计学分析。计量资料符合正态分布时用
$(\bar x \pm s)$ 表示,符合非正态分布时采用M(Q)表示;组间一般临床资料和肺功能差异采用独立样本t检验、Mann-Whitney U检验或卡方检验;采用Spearman相关分析吸气相LAA%-950、呼气相LAA%-910、PRMEmph%与FVC、FEV1%、FEV1/FVC的相关性。绘制受试者工作特征(receiver operating characteristic curve,ROC)曲线分析CT定量参数对轻中度COPD患者肺气肿评估的诊断效能。P<0.05有统计学意义。2. 结果
2.1 一般资料比较
轻中度COPD患者与正常对照组,年龄、BMI及FVC组间无统计学差异;正常对照组女性占比显著低于轻中度COPD患者,轻中度COPD患者吸烟指数较正常对照组增大,轻中度COPD患者FEV1%、FEV1/FVC数值小于正常对照组,组间存在统计学差异(表1)。
表 1 一般资料结果比较Table 1. Comparison of general information and results项目 正常对照组(n=55) 轻中度COPD患者(n=52) 统计检验 $t/ {\chi }^{2}/Z $ P 年龄/岁 58.130±8.228 58.700±9.622 -0.735 0.464 性别(男/女) 53/2 40/12 8.883 0.003 BMI/(kg/m2) 24.573±2.975 23.380±2.507 1.684 0.096 吸烟指数 400.000(392.000) 655.000(800.000) -3.327 0.001 FVC/L 3.461±0.769 3.270±1.052 1.248 0.215 FEV1%/% 81.570±14.395 69.640±13.654 3.008 0.003 FEV1/FVC/% 81.030±10.000 58.880±9.771 12.236 <0.001 注:正态资料用$\bar{x}$±s表示,偏态资料用M(Q)表示。 2.2 组间CT定量指标比较
轻中度COPD患者相比于正常对照组,吸气相LAA%-950、呼气相LAA%-910、PRMEmph%、PRMfSAD%四项指标均增大,PRMNormal%减小,且组间差异均有统计学意义(表2、图2和图3)。
表 2 正常对照与轻中度COPD组间CT定量指标比较Table 2. Comparison of CT quantitative indexes between the normal control and mild to moderate COPD groups项目 正常对照组(n=55) 轻中度COPD患者(n=52) 统计检验 Z P 吸气相LAA%-950/% 19.210(7.890) 28.160(12.080) -4.323 <0.001 呼气相LAA%-910/% 10.380(10.360) 26.210(26.680) -6.439 <0.001 PRMEmph%/% 4.055(3.570) 15.610(18.590) -6.697 <0.001 PRMfSAD%/% 14.685(11.640) 27.810(15.280) -4.806 <0.001 PRMNormal%/% 59.615(15.120) 37.340(37.490) -5.273 <0.001 注:偏态资料用M(Q)表示。 ![]() 图 3 男,63岁,GOLD 2级。正常对照受试者与轻中度COPD患者PRMEmph%(红色区域)存在差异,轻中度COPD患者病变明显加重Figure 3. Male, 63 years old, GOLD grade 2. There was a difference in PRMEmph% (red area) between normal controls and patients with mild to moderate COPD, and the lesions of patients with mild to moderate COPD were significantly aggravated
图 3 男,63岁,GOLD 2级。正常对照受试者与轻中度COPD患者PRMEmph%(红色区域)存在差异,轻中度COPD患者病变明显加重Figure 3. Male, 63 years old, GOLD grade 2. There was a difference in PRMEmph% (red area) between normal controls and patients with mild to moderate COPD, and the lesions of patients with mild to moderate COPD were significantly aggravated2.3 CT定量参数与PFT的相关性
呼气相LAA%-910、PRMEmph%与 FVC、FEV1%、FEV1/FVC均呈负相关,吸气相LAA%-950与 FEV1/FVC呈负相关,吸气相LAA%-950与FVC、FEV1% 无线性相关(表3)。
表 3 CT定量参数与肺功能的相关性Table 3. Correlations between CT quantitative parameters and pulmonary functionCT定量参数 相关系数及其检验rS(P) FVC/L FEV1%/% FEV1/FVC/% 吸气相LAA%-950/% 0.044(0.655) -0.150(<0.122) -0.512(<0.001) 呼气相LAA%-910/% -0.301(0.002) -0.394(<0.001) -0.668(<0.001) PRMEmph%/% -0.269(0.005) -0.361(<0.001) -0.696(<0.001) 2.4 CT定量参数区分正常人群与轻中度COPD患者的价值
吸气相LAA%-950、呼气相LAA%-910、PRMEmph%区分轻中度 COPD的曲线下面积分别为0.742、0.861和0.876,其中PRMEmph%指标的曲线下面积最大,对应的临界值为9.84%,敏感度76.90%,特异度94.50%(图4)。
3. 讨论
COPD的特征是呼吸道和肺实质的慢性炎症,不可避免地导致(部分不可逆的)肺改变。胸部CT的发展为COPD疾病异质性了解提供新的视角。目前CT检查是COPD患者重要的影像学检查方法[18],且双气相CT定量参数是COPD患者肺气肿的重要指标,CT上肺气肿范围的改变可以预测COPD患者的死亡率,因此为早期COPD筛选出最优CT定量肺气肿指标有重要意义[19-20]。
本研究结果显示年龄与BMI组间无统计学差异,减小了由年龄与BMI对组间受试者的影响。组间性别有差异,轻中度COPD患者组女性占比显著高于正常对照组,轻中度COPD患者的吸烟指数显著高于正常对照组。结果说明女性较男性更容易受到吸烟的有害影响[21-22],吸烟是导致COPD的危险因素之一,故年龄高于40岁且吸烟的人群是COPD的易感人群[1],通过双气相CT定量可以更好的评估病变程度。
本研究使用吸气相LAA%-950、呼气相LAA%-910、PRMEmph%来研究COPD患者肺气肿的诊断效能,其中PRMEmph%不仅可以区分COPD的主要病理生理学(肺气肿)改变,还可以可视化定量分析正常区域、功能性小气道区域及肺气肿区域等。既往研究[23]表明吸气相 LAA%-950是量化肺气肿的最佳阈值,且与肺功能相关性良好。本文中呼气相LAA%-910与 FEV1% 的相关性最高,而FEV1% 是COPD分级的指标,因此可以说明呼气相LAA%-910对评估COPD的严重程度比较敏感,这与本团队之前的研究[12]结果一致。双气相定量PRM能够可视化及量化肺气肿的改变,与肺功能指标相关联[24],另有研究证实PRMEmph%与肺气肿相关,且与吸气相LAA%-950、呼气相LAA%-910两项指标相比,PRMEmph%与FEV1/FVC相关性更好[9-25]。吸气相LAA%-950、呼气相LAA%-910、PRMEmph%3项指标分别区分正常对照组和 COPD轻中度患者的肺气肿,ROC结果的曲线下面积分别为0.742、0.861和0.876,并且都有一定意义,诊断效能均比较好。其中PRMEmph%的AUC最大,且考虑到其包含的信息较多,诊断效能优于吸气相LAA%-950和呼气相LAA%-910。
本研究在相关分析的基础上绘制了ROC曲线,结果论证了双气相配准指标优于单气相指标。由于肺气肿是COPD中晚期的主要病变,目前对早期COPD的研究主要是小气道,而本研究主要针对轻中度COPD患者的肺气肿情况,寻找诊断轻中度COPD患者肺气肿的最优定量CT指标,而筛选最优肺气肿定量分析指标也是本研究最大创新点。
本研究团队之前的研究表明呼气相LAA%-910是准确评估COPD严重程度的敏感指标,并且与临床肺功能具有良好的相关性,这与本研究的结论一致,可以对COPD患者进行更全面的评估提供参考[15]。研究表明[26]PRM增加了目前已知的CT测量在诊断COPD方面的价值,其与临床参数的强相关性表明,PRM可以提供关于疾病表型和严重程度的重要信息。因此PRM的优点是能够区分肺气肿和非肺气肿的空气滞留,从而能够更真实地评估COPD患者的肺气肿情况。PRMEmph%可以区分以肺气肿为特征的COPD的临床异质性,这是PRM的一个重要特征,因为不同的表型可能会有不同的生命过程及结果,因此可以用来确定患者的特征,且可以为不能行肺功能检查的患者进行肺功能的检测及分级,并在未来制定个性化治疗方案。
随着胸部低剂量CT技术的发展,不仅应用于肺癌筛查,也可用于肺部其他疾病,对于COPD易感人群行双气相扫描也符合伦理要求[10],定量CT可以更加精确、客观的分析肺部异常,在早期有效的发现病变,且可用于不能进行肺功能检查的特殊人群。综上,我们认为PRM是一种很有前途且优于单气相的CT指标。
本研究的局限性是样本量较少,后续研究可以增加样本量,尤其是女性患者,对COPD患者进行性别分组研究。此外,本研究只区分正常对照组和轻中度COPD患者,之后可以进行跟踪随访,进一步对疾病严重程度进行诊断。
综上所述,吸气相LAA%-950、呼气相LAA%-910、PRMEmph%都能很好地诊断轻中度COPD患者的肺气肿,其中PRMEmph%可以更为准确、敏感地识别轻中度COPD患者肺气肿的改变,可作为轻中度COPD患者肺气肿诊断的可靠指标,有效的应用于临床实践。
-
表 1 定量指标结果
Table 1 Quantitative results
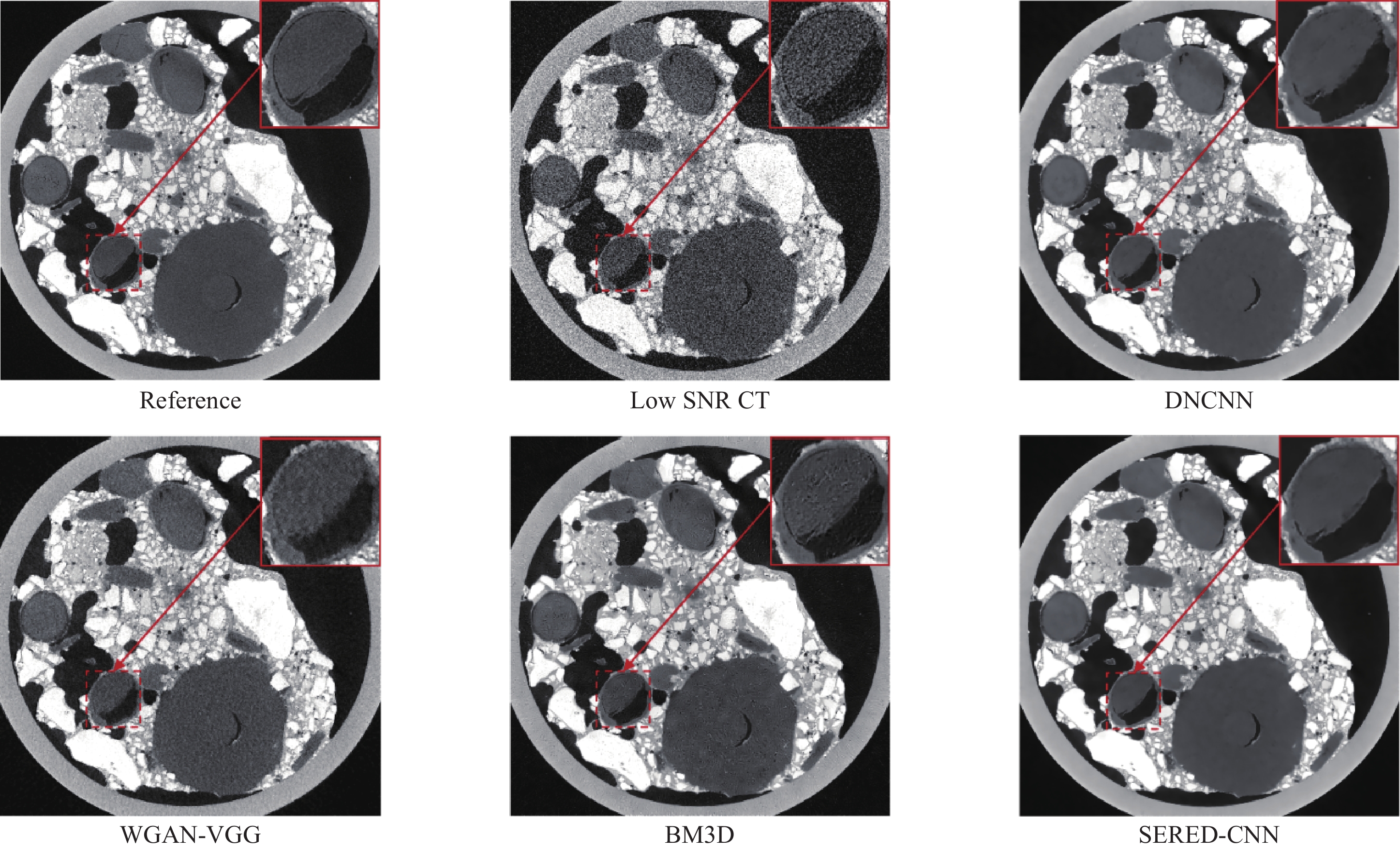
定量指标 Low SNR CT DNCNN WGAN-VGG BM3D Our method PSNR 32.1306 39.3383 34.7620 37.9226 40.8110 SSIM 0.6657 0.9409 0.8463 0.9012 0.9475 RMSE 0.0124 0.0054 0.0091 0.0064 0.0046 表 2 消融实验定量指标结果
Table 2 Quantitative results of ablation experiments
定量指标 Low SNR CT RED-CNN Our method PSNR 32.1306 40.7895 40.8110 SSIM 0.6657 0.9476 0.9475 RMSE 0.0124 0.0046 0.0046 -
[1] BRENNER D J, ELLISTON C D, HALL E J, et al. Estimated risks of radiation-induced fatal cancer from pediatric CT[J]. American journal of roentgenology, 2001, 176(2): 289-296. DOI: 10.2214/ajr.176.2.1760289.
[2] BRENNER D J, HALL E J. Computed tomography—an increasing source of radiation exposure[J]. New England Journal of Medicine, 2007, 357(22): 2277-2284. DOI: 10.1056/NEJMra072149.
[3] DE CHIFFRE L, CARMIGNATO S, KRUTH J P, et al. Industrial applications of computed tomography[J]. CIRP annals, 2014, 63(2): 655-677. DOI: 10.1016/j.cirp.2014.05.011.
[4] IZUMI S, KAMATA S, SATOH K, et al. High energy X-ray computed tomography for industrial applications[J]. IEEE transactions on nuclear science, 1993, 40(2): 158-161. DOI: 10.1109/23.212333.
[5] HIGAKI T, NAKAMURA Y, FUKUMOTO W, et al. Clinical application of radiation dose reduction at abdominal CT[J]. European Journal of Radiology, 2019, 111: 68-75. DOI: 10.1016/j.ejrad.2018.12.018.
[6] NATTERER F. The mathematics of computerized tomography[M]. Society for Industrial and Applied Mathematics, 2001.
[7] WILLEMINK M J, NOëL P B. The evolution of image reconstruction for CT-from filtered back projection to artificial intelligence[J]. European radiology, 2019, 29: 2185-2195. DOI: 10.1007/s00330-018-5810-7.
[8] ANDERSEN A H, KAK A C. Simultaneous algebraic reconstruction technique (SART): A superior implementation of the ART algorithm[J]. Ultrasonic imaging, 1984, 6(1): 81-94. DOI: 10.1177/016173468400600107.
[9] SIDKY E Y, PAN X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J]. Physics in Medicine & Biology, 2008, 53(17): 4777.
[10] DONOHO D L. Compressed sensing[J]. IEEE Transactions on information theory, 2006, 52(4): 1289-1306. DOI: 10.1109/TIT.2006.871582.
[11] CHEN Z, JIN X, LI L, et al. A limited-angle CT reconstruction method based on anisotropic TV minimization[J]. Physics in Medicine & Biology, 2013, 58(7): 2119.
[12] GONG C, ZENG L, WANG C. Image reconstruction model for limited-angle CT based on prior image induced relative total variation[J]. Applied Mathematical Modelling, 2019, 74: 586-605. DOI: 10.1016/j.apm.2019.05.020.
[13] LUO F, LI W, TU W, et al. Adaptive weighted total variation minimization based alternating direction method of multipliers for limited angle CT reconstruction[J]. IEEE Access, 2018, 6: 64225-64236. DOI: 10.1109/ACCESS.2018.2873713.
[14] LIU Y, MA J, FAN Y, et al. Adaptive-weighted total variation minimization for sparse data toward low-dose x-ray computed tomography image reconstruction[J]. Physics in Medicine & Biology, 2012, 57(23): 7923.
[15] YU W, ZENG L.
${l_0}$ gradient minimization based image reconstruction for limited-angle computed tomography[J]. PloS one, 2015, 10(7): e0130793. DOI: 10.1371/journal.pone.0130793.[16] WANG T, WANG C, ZHAO K, et al. Guided image filtering based
${l_0}$ gradient minimization for limited-angle CT image reconstruction[J]. Journal of Inverse and Ill-posed Problems, 2021, 29(4): 587-598.[17] WANG C, LUO X, YU W, et al. A variational proximal alternating linearized minimization in a given metric for limited-angle CT image reconstruction[J]. Applied Mathematical Modelling, 2019, 67: 315-336. DOI: 10.1016/j.apm.2018.09.038.
[18] ZHANG Y, DONG B, LU Z. Minimization for wavelet frame based image restoration[J]. Mathematics of Computation, 2013, 82(282): 995-1015.
[19] ZHOU W, CAI J F, GAO H. Adaptive tight frame based medical image reconstruction: A proof-of-concept study for computed tomography[J]. Inverse problems, 2013, 29(12): 125006. DOI: 10.1088/0266-5611/29/12/125006.
[20] WANG C, ZENG L, GUO Y, et al. Wavelet tight frame and prior image-based image reconstruction from limited-angle projection data[J]. Inverse Problems and Imaging, 2017, 11(6): 917-948. DOI: 10.3934/ipi.2017043.
[21] WANG G. A perspective on deep imaging[J]. IEEE access, 2016, 4: 8914-8924. DOI: 10.1109/ACCESS.2016.2624938.
[22] 朱元正, 吕启闻, 官瑜, 等. 基于深度能量模型的低剂量CT重建[J]. CT理论与应用研究, 2022, 31(6): 709-720. DOI: 10.15953/j.ctta.2021.077. ZHU Y Z, LV Q W, GUAN Y, et al. Low-dose CT reconstruction based on deep energy models[J]. CT Theory and Applications, 2022, 31(6): 709-720. DOI: 10.15953/j.ctta.2021.077.
[23] CHEN H, ZHANG Y, ZHANG W, et al. Low-dose CT via convolutional neural network[J]. Biomedical optics express, 2017, 8(2): 679-694. DOI: 10.1364/BOE.8.000679.
[24] ZHANG K, ZUO W, CHEN Y, et al. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising[J]. IEEE transactions on image processing, 2017, 26(7): 3142-3155. DOI: 10.1109/TIP.2017.2662206.
[25] RONNEBERGER O, FISCHER P, BROX T. U-net: Convolutional networks for biomedical image segmentation[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer International Publishing, 2015: 234-241.
[26] 樊雪林, 文昱齐, 乔志伟. 基于Transformer增强型U-net的CT图像稀疏重建与伪影抑制[J]. CT理论与应用研究(中英文), 2024, 33(1): 1-12. DOI: 10.15953/j.ctta.2023.183. FAN X L, WEN Y Q, QIAO Z W. Sparse reconstruction of computed tomography images with transformer enhanced U-net[J]. CT Theory and Applications, 2024, 33(1): 1-12. DOI: 10.15953/j.ctta.2023.183.
[27] CHEN H, ZHANG Y, KALRA M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network[J]. IEEE transactions on medical imaging, 2017, 36(12): 2524-2535. DOI: 10.1109/TMI.2017.2715284.
[28] OKTAY O, SCHLEMPER J, FOLGOC L L, et al. Attention u-net: Learning where to look for the pancreas[J]. arxiv preprint arxiv: 1804.03999, 2018.
[29] HU J, SHEN L, SUN G. Squeeze-and-excitation networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 7132-7141.
[30] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[J]. Advances in neural information processing systems, 2014, 27.
[31] WOLTERINK J M, LEINER T, VIERGEVER M A, et al. Generative adversarial networks for noise reduction in low-dose CT[J]. IEEE transactions on medical imaging, 2017, 36(12): 2536-2545. DOI: 10.1109/TMI.2017.2708987.
[32] YANG Q, YAN P, ZHANG Y, et al. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss[J]. IEEE transactions on medical imaging, 2018, 37(6): 1348-1357. DOI: 10.1109/TMI.2018.2827462.
[33] LI Z, HUANG J, YU L, et al. Low-dose CT image denoising using cycle-consistent adversarial networks[C]//2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). IEEE, 2019: 1-3.
[34] FERUGLIO P F, VINEGONI C, GROS J, et al. Block matching 3D random noise filtering for absorption optical projection tomography[J]. Physics in Medicine & Biology, 2010, 55(18): 5401.
[35] KANG D, SLOMKA P, NAKAZATO R, et al. Image denoising of low-radiation dose coronary CT angiography by an adaptive block-matching 3D algorithm[C]//Medical Imaging 2013: Image Processing. SPIE, 2013, 8669: 671-676.
[36] AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on signal processing, 2006, 54(11): 4311-4322. DOI: 10.1109/TSP.2006.881199.
[37] SHI J, ELKILANY O, FISCHER A, et al. Lodoind: introducing a benchmark low-dose industrial CT dataset and enhancing denoising with 2.5D deep learning techniques[C]//13th Conference on Industrial Computed Tomography (iCT), Wels Campus, Austria. 2024, 10: 29228.




 下载:
下载: