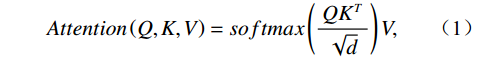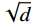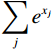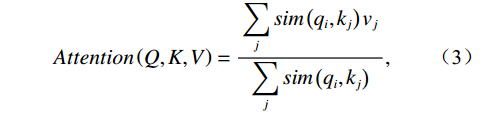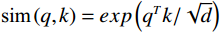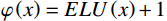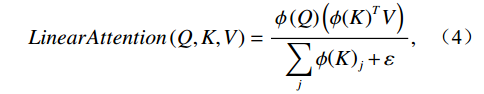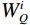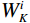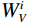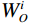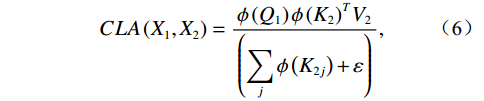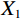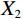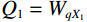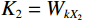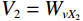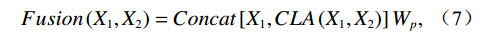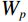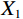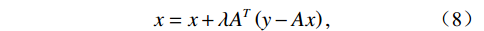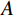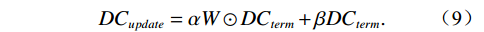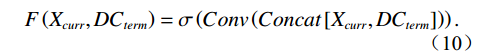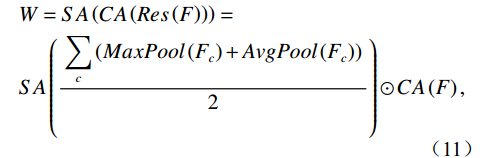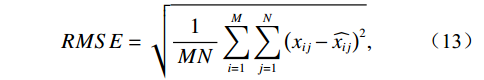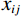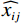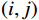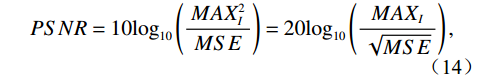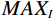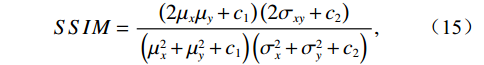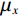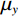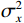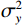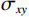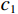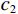CT serves as one of the most essential imaging tools in modern medical diagnosis, playing an irreplaceable role in clinical practice. However, X-ray radiation during CT imaging poses carcinogenic risks. To reduce radiation exposure to patients, sparse-view CT imaging technique has emerged as a solution, which reduces total radiation dose by decreasing the number of projections. While this approach effectively lowers the radiation dose, it poses challenges for image reconstruction due to incomplete projection data. Traditional analytical reconstruction methods are represented by the filtered back projection (FBP) algorithm. Although FBP features fast computation and easy implementation, making it the mainstream algorithm in commercial CT systems, its performance heavily depends on the completeness of projection data. Under sparse-view sampling conditions, FBP-reconstructed images often exhibit prominent streak artifacts, severely compromising diagnostic quality.

Research in sparse-view CT image reconstruction has evolved through three main approaches: iterative reconstruction, deep learning methods, and their integration. As a fundamental approach, iterative reconstruction methods effectively handle incomplete projection data by establishing an optimization framework between image and projection domains. At its core, this method combines data consistency constraints with regularization terms such as total variation (TV), where the data consistency ensures fidelity to measured projections while regularization helps suppress noise and artifacts, ultimately enabling high-quality reconstruction from sparse-view data. In 2006, Sidky, Pan, and colleagues proposed a sparse-view reconstruction method using total variation algorithms for divergent-beam CT imaging^[1]. They further developed this in 2008 with the Adaptive-Steepest-Descent-Projection-Onto-Convex-Sets (ASD-POCS) algorithm^[2], achieving quality reconstruction with only 20-view projections even with Gaussian noise. Several important variants of TV have been proposed: Do et al. introduced higher-order TV (HOTV) to reduce staircase artifacts^[3]. Tian et al. proposed edge-preserving TV (EPTV) for low-contrast CT imaging^[4]. Liu et al. developed adaptive-weighted TV (AwTV) to address edge over-smoothness^[5]. Xu et al. proposed relative total variation (RTV) for structure extraction under texture^[6]. NING et al. developed an lp norm compressive sensing approach^[7]. Sidky et al. proposed total p variation (TpV) solved via Chambolle-Pock^[8]. Rigie et al. introduced total nuclear variation (TnV) for better boundary preservation^[9]. More recently, Zhang et al. proposed directional total variation (DTV) to preserve structural features^[10]. Qiao developed a simplified ASD-POCS algorithm^[11] and introduced balanced total variation (bTV) for fast convergence in EPRI^[12] and directional TV method for sparse-view EPRI^[13]. In 2025, Jiang et al. proposed a non-local total generalized variation (NLTGV) regularization method for sparse-view CT reconstruction, combining non-local self-similarity with variational information to enhance image quality^[14]. However, iterative reconstruction methods face two major limitations: high computational cost resulting in long reconstruction times, and the difficulty in selecting optimal parameters, which has hindered their widespread clinical adoption.

Deep learning has introduced novel approaches to sparse-view CT reconstruction. As Wang highlighted in review, the intersection of X-ray imaging and deep learning presents tremendous synergistic effects and countless opportunities in this rapidly evolving field^[15]. U-Net-based architectures have demonstrated particular effectiveness in artifact removal. In 2015, Ronneberger et al. proposed the U-Net with an encoder-decoder structure that was adapted from image segmentation to reconstruction^[16]. In 2016, Han et al. developed a U-Net -based deep residual learning method for streak artifact removal^[17]. In 2017, Jin et al. introduced FBPConvNet combining residual U-Net with FBP^[18], achieving superior results over TV methods. Chen et al. proposed RED-CNN integrating residual learning through deconvolution and shortcut connections^[19]. In 2018, Steven Guan introduced FD-U-Net with dense connections to reduce parameters while maintaining performance^[20]. In 2020, Zheng et al. proposed a dual-domain deep learning method^[21]. In 2022, Kandarpa et al. proposed a CED network using low-resolution scout images^[22]. In 2023, Yu et al. proposed an unsupervised dual-domain method combining Noise2 Self and iterative enhancement^[23]. Zhu et al. proposed an energy-based deep model for low-dose CT reconstruction by learning prior knowledge from normal-dose CT images^[24]. In 2024, Han et al. proposed a theoretically justified dual-domain deep learning framework^[25]. The Transformer architecture has opened new possibilities in computer vision through self-attention mechanisms, which enable global context modeling and capture long-range dependencies that are crucial for preserving structural details in images. In 2017, Vaswani et al. first proposed the Transformer model based on attention mechanisms^[26], while Dosovitskiy et al. later adapted it for vision tasks through the Vision Transformer (ViT) model in 2020^[27]. The successful application of Transformers has also benefited CT image reconstruction. In 2022, Qiao et al. proposed a CNN transformer coupling network (CTC) that combines the local feature extraction capabilities of CNN with the global information capture abilities of transformer for low-dose CT image denoising^[28]. in 2023, Liu et al. proposed the D-U-Transformer network combining dense connections and Transformers^[29], while Yan et al. introduced CGP-Uformer with innovative channel graph perception blocks for low-dose CT denoising^[30]. Fan et al. proposed a Transformer Enhanced U-Net (TE-unet) that combines CNN with multiple attention mechanisms to effectively suppress stripe artifacts^[31]. Li et al. proposed MDST, a multi-domain transformer network with improved detail preservation^[32]. To address computational complexity issues, researchers have proposed various improvements: McKerahan et al. introduced linear attention mechanisms^[33], Wang et al. developed Linformer with dimensionality reduction^[34], Choromanski et al. proposed the Performer model using random feature mapping^[35], and Shen et al. introduced Efficient Attention^[36]. In 2020, Katharopoulos et al. reformulated self-attention using kernel features^[37]. However, these pure deep learning approaches still face challenges. Their "black box" nature makes it difficult to interpret the reconstruction process, while their limited generalization capability can lead to degraded performance when encountering data distributions different from the training set. Moreover, these approaches lack physical consistency guarantees in their reconstructions.

Recent years have witnessed progress in combining iterative reconstruction with deep learning approaches. In 2018, Chen et al. proposed the LEARN network^[38], which introduced “expert domain” generalized regularization terms into sparse-view iterative reconstruction models using CNN modules for parameter learning and updating. This pioneered adaptive adjustment of data consistency constraints. Moreover, Zhang et al. also extended the LEARN model to a dual-domain version, called LEARN++^[39]. In the same year, Yu et al. developed the Deep Cascaded CNN (DC-CNN)^[40], achieving gradual optimization of data consistency through cascaded modules while maintaining reconstruction quality. In 2019, Aggarwal et al. introduced MoDL with learnable data consistency layers that automatically adjust constraint strength^[41], while Wang et al. proposed ADMMBDR incorporating U-Net into ADMM iterations for limited-angle CT^[42]. Liao et al. presented ADN for more precise consistency constraints through explicit artifact modeling^[43]. In 2020, Putzky and Welling developed RIM combining data consistency learning with recurrent networks^[44]. In 2021, Xiang et al. introduced FISTA-net combining the FISTA algorithm with CNN for accelerated convergence^[45], while Wu et al. integrated residual U-Net and GAN with compressed sensing for dual-domain processing optimization^[46]. In 2022, Genzel et al. proposed an iterative neural network ItNet^[47], Su et al. proposed a generalized unrolling scheme that learns iteration parameters, regularizer and data-fidelity terms^[48]. Jia et al. proposed a superiorization-inspired unrolled SART algorithm with U-Net generated perturbations^[49]. In 2024, Sun et al. proposed an efficient dual-domain deep unrolling network by alternating optimization between dense-view sinograms and images^[50]. While these integrated approaches have shown promising results, most existing methods rely heavily on convolutional neural networks (CNNs) for feature extraction. Although CNNs are computationally efficient and effective at capturing local patterns, they inherently lack the ability to model long-range dependencies in image features due to their limited receptive fields. This limitation can affect the network’s capacity to preserve global structural information and handle complex artifacts that span across large image regions. The Transformer architecture, with its self-attention mechanism, offers a solution by enabling global context modeling. However, the direct application of Transformers in medical image reconstruction faces computational challenges - the standard self-attention mechanism has quadratic complexity with respect to the spatial dimensions of feature maps, making it prohibitively expensive for high-resolution medical images. To address this computational bottleneck while still leveraging the advantages of Transformers, we propose incorporating linear attention mechanisms that reduce the computational complexity from quadratic to linear.

To efficiently achieve higher reconstruction accuracy, this paper proposes TransitNet, a deep neural network based on iterative unrolling, which fully leverage the advantages of both data-driven and model-driven approaches. This method builds upon an iterative reconstruction framework, incorporating Transformers in each iteration to enhance image feature extraction capabilities while ensuring physical reliability of reconstruction results through learnable data consistency operations. Specifically, the main contributions of this paper include:

1. We Design a novel iterative neural network architecture that organically integrates model-driven data consistency, a physical a prior constraint, with deep learning’s feature extraction capabilities.

2. We introduce Transformer mechanisms with linear attention to enhance feature extraction and model long-range dependencies while reducing computational complexity from quadratic to linear.

3. We propose learnable data consistency operations that achieve more flexible physical constraints through adaptive adjustment of global and local parameters.

4. We conducted extensive experiments to validate the superior performance of our proposed method compared to existing approaches in sparse-view reconstruction tasks.

1.   Methods

1.1   Iterative Framework

Iterative reconstruction progressively improves image quality through multiple rounds of optimization. Each iteration consists of two key steps: image enhancement and data consistency correction. The image enhancement step is responsible for improving the quality of reconstructed images. While traditional methods primarily rely on mathematical models such as total variation regularization, the advancement of deep learning has enabled the use of neural networks as image enhancers. The powerful feature extraction capabilities of neural networks allow them to intelligently distinguish between noise and useful information. However, in medical CT image processing, special attention must be paid to preserving diagnostically relevant details while avoiding over-processing. In data consistency correction, the current reconstructed image is first forward-projected to obtain simulated projection data, which is then compared with actual measured data to determine discrepancies. These discrepancies are transformed back to the image domain through back-projection, creating a difference image used to update the reconstruction results. Weight parameters are introduced during the update process to balance convergence speed and stability.

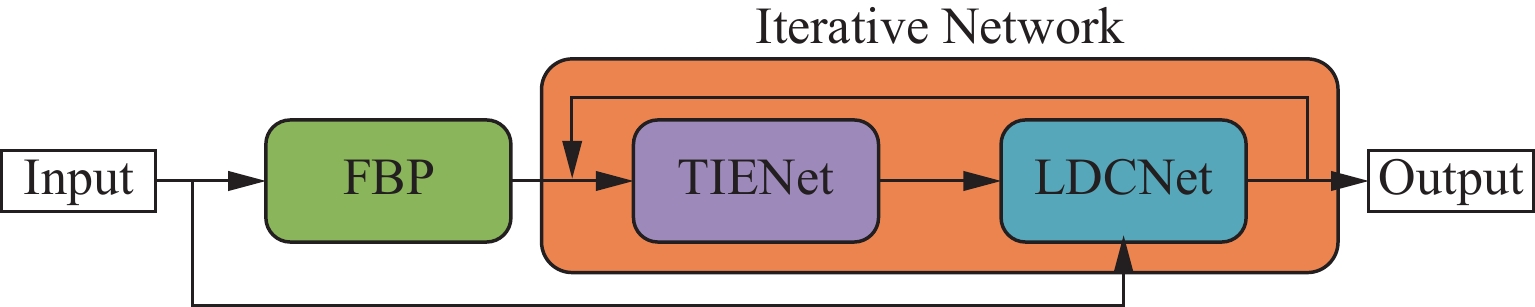
The proposed TransitNet iterative reconstruction framework is inspired by ItNet^[47], which is an iterative neural network specifically designed for CT image reconstruction problems. It improves reconstruction quality by replacing computational steps in traditional iterative algorithms with learnable neural networks. In each iteration, the TransitNet network performs two main steps: first, it processes the reconstructed image using an image enhancement subnetwork (TIENet) to improve the reconstruction quality; then it performs data consistency correction (LDCNet) to adjust the reconstruction results based on discrepancies with actual measured data. Figure 1 shows the entire framework structure:

Figure  1.  TransitNet Structure

下载: 全尺寸图片 幻灯片

This iterative framework combining deep learning maintains the constraints of physical models, ensuring consistency between reconstruction results and measured data, while fully leveraging the powerful feature extraction capabilities of neural networks. Particularly in challenging scenarios such as low-dose imaging or incomplete data, it can achieve better results than traditional reconstruction methods. Building upon this framework, this paper will introduce improved feature extraction modules and data consistency operations to further enhance reconstruction performance.

1.2   Image Enhancement Network with Transformer Integration

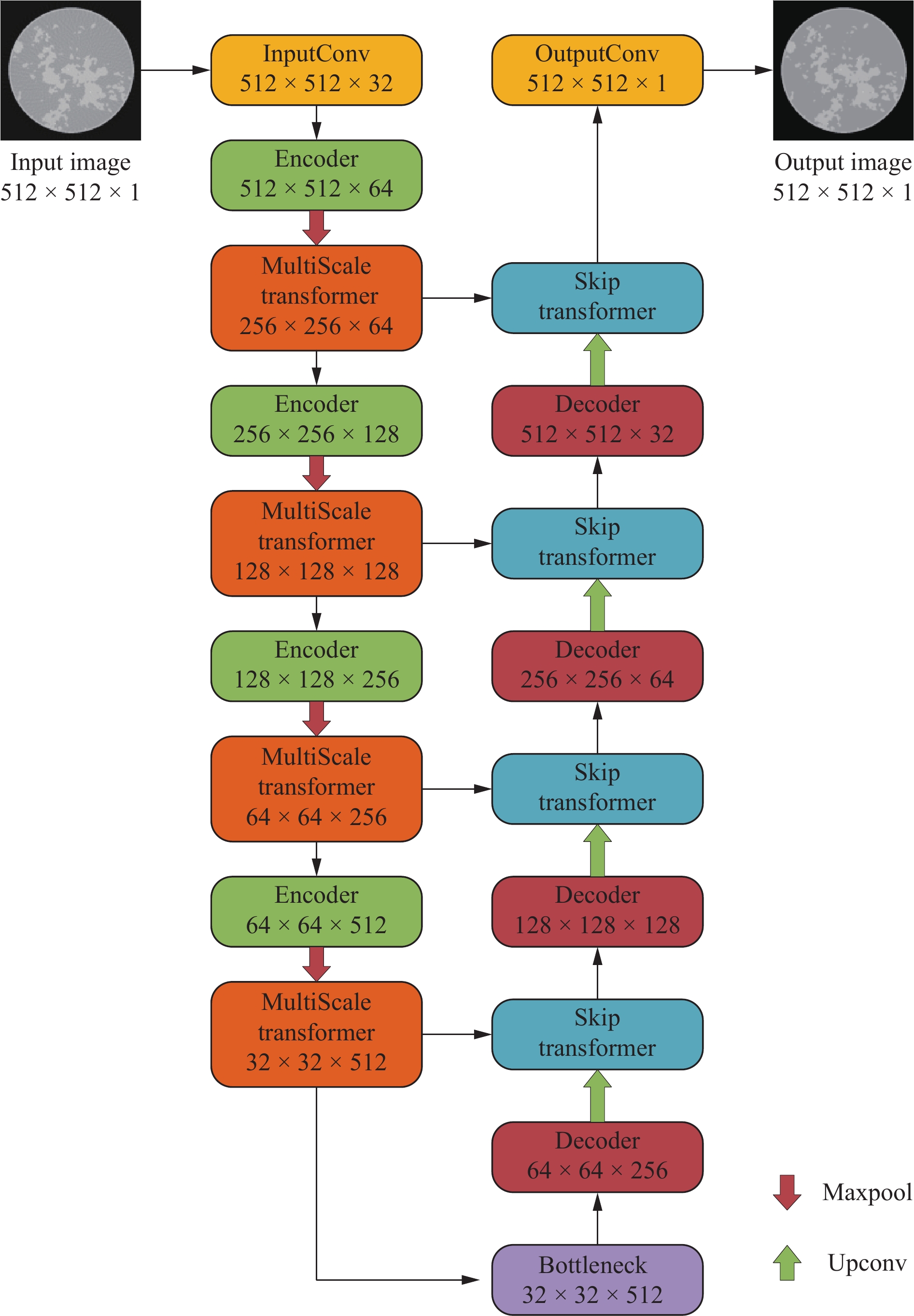
In the iterative framework, we designed a U-shaped network (U-Net) incorporating Transformer mechanisms as the image enhancement subnetwork (TIENet). While maintaining the classic encoder-decoder structure of U-Net, this network innovatively introduces multi-scale Transformer and cross-domain attention mechanisms to enhance feature extraction and information transmission capabilities. The structure of TIENet network is shown in Figure 2:

Figure  2.  TIENet Structure

下载: 全尺寸图片 幻灯片

In the encoder section, the network starts with the input channels, setting the base feature channel number to 32, then progressively doubles the channel numbers across four encoding blocks. Each encoding block employs 3×3 convolution kernels with padding of 1 to maintain feature map dimensions. The group normalization uses 32 groups, which ensures effective normalization even with small batch sizes. The multi-scale Transformer module is configured with 8 attention heads, a window size of 8, and an MLP expansion ratio of 4, enabling feature relationship capture at different scales. The bottleneck layer maintains the same channel number as the final encoding block, utilizing identical convolution and normalization configurations for further feature processing. In the decoder section, four decoding blocks progressively upscale the feature map dimensions through transposed convolution, halving the channel numbers sequentially. The transposed convolution employs 3×3 kernels with a stride of 2 for upsampling. The cross-layer attention module also utilizes 8 attention heads, computing attention weights through linear projections to effectively fuse encoder and decoder features. The final output layer maps the feature maps to the specified output channels using 1×1 convolution. Throughout the network, the dropout ratio can be flexibly adjusted to control regularization intensity.

To address the quadratic computational complexity of standard Transformers in processing high-resolution medical images, this work implements an improved linear attention mechanism that operates in two key aspects: multi-scale feature extraction and cross-domain feature fusion. For multi-scale processing, the network utilizes LinearWindowAttention, which partitions input features into fixed-size windows and computes attention within each window using ELU activation and matrix multiplication instead of traditional softmax operations. For feature fusion, LinearMultiHeadCrossAttention is employed at skip connections to efficiently merge encoder and decoder features through linear projections and correlations. This dual-purpose linear attention approach reduces computational overhead while maintaining effective feature extraction and adaptive feature fusion capabilities.

The linear attention mechanism used in this paper is based on Fast Autoregressive Transformers with Linear Attention proposed by Katharopoulos et al.^[37], which represents self-attention as a linear dot product of kernel feature maps and use the associativity property of matrix products to reduce the complexity from O(N²) to O(N)，where N is the sequence length.

First, the computational formula for traditional attention mechanism is:

where Q (Query), K (Key), and V (Value) are learnable matrices representing different aspects of the input features, and d is the dimension of the key vectors. Q interacts with K to compute attention scores, which are then applied to V to produce the weighted output. The $ \sqrt{d} $ term helps stabilize training by preventing the dot products from becoming too large.

The core function of softmax is to normalize attention scores. Specifically, softmax maps arbitrary real numbers to the interval (0,1) with a sum of 1:

where xi represents the input value at position i, and the denominator ${\displaystyle\sum _{j}{e}^{{x}_{j}}} $ sums up the exponentials of all values in the sequence, ensuring that the outputs are normalized to sum to 1.

However, this nonlinear transformation requires computing the exponential sum over the entire sequence, resulting in a computational complexity of O(N²). Based on kernel method theory, we can reformulate the attention mechanism in terms of kernel functions:

where sim is the similarity function. When choosing $ \text{sim}\left(q,k\right)=exp\left({q}^{T}k/\sqrt{d}\right) $, it corresponds to standard softmax attention. Based on kernel function equivalence, we can use $ \varphi\left(x\right)=ELU\left(x\right)+1 $ as the feature mapping function to rewrite the attention computation as:

where $ {\phi } $ denotes the feature mapping function, ε is a small constant to ensure numerical stability, and the denominator $ \displaystyle \sum _{j}{\phi }{\left(K\right)}_{j} $is to normalize attention scores. Meanwhile, the computational mechanisms of each Transformer module will undergo corresponding modifications. The multi-scale Transformer component consists of attention computation and multi-head attention integration, calculated as follows:

where h is the number of attention heads, $ {W}_{Q}^{i} $, $ {W}_{K}^{i} $, $ {W}_{V}^{i} $ are the linear transformation matrices for the i-th head, and $ {W}_{O}^{i} $ is the output projection matrix for the i-th head.

The cross-domain attention module includes cross-attention computation and cross-layer feature fusion, calculated as follows:

where $ {X}_{1} $ and $ {X}_{2} $ represent low-level and high-level features respectively, $ {Q}_{1}={W}_{q{X}_{1}} $ is the query transformation of low-level features, and $ {K}_{2}={W}_{k{X}_{2}} $, $ {V}_{2}={W}_{v{X}_{2}} $ are the key-value transformations of high-level features.

where Concat represents the concatenation operation along the channel dimension, $ {W}_{p} $ is the final projection matrix, $ {X}_{1} $ represents low-level features, and $ {X}_{2} $ represents high-level features.

Convolutional operations excel at extracting local features, while Transformer mechanisms are adept at establishing long-range dependencies. The combination of these two enables the network to perform exceptionally well in preserving detailed structures and suppressing noise. Finally, the features are mapped to the output space through a 1×1 convolutional layer to complete the image enhancement task.

1.3   Learnable Data Consistency

Data consistency operation is a crucial step in CT image reconstruction, with its core concept being to ensure consistency between the reconstructed image and actual measured data in the projection domain. Traditional data consistency operations project the reconstructed image into the sinogram domain through Radon transform, compute the residual with measured data, and then map the residual back to the image domain through back-projection for updates. This process can be expressed as:

where x is the reconstructed image, y is the measured data, $ A $ and $ {A}^{T} $ are the forward and backward projection operators respectively, and λ is the weight coefficient controlling the update step size.

To enhance the adaptability and performance of data consistency operations, this paper proposes a learnable data consistency network structure (Learnable Data Consistency Net, LDCNet). This network first concatenates the current reconstructed image and data consistency term along the channel dimension, processing them through a feature extraction network. The feature extraction network employs a residual structure and dual attention mechanism, where the residual structure facilitates learning residual information and prevents gradient vanishing, while the channel attention and spatial attention mechanisms adaptively adjust the importance of features.

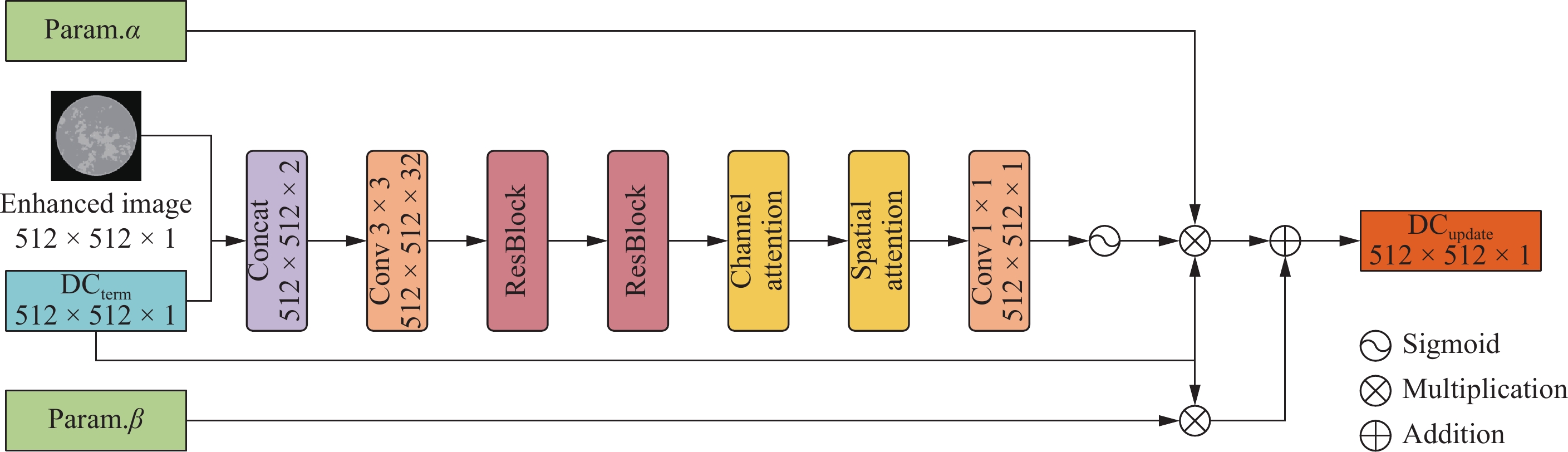
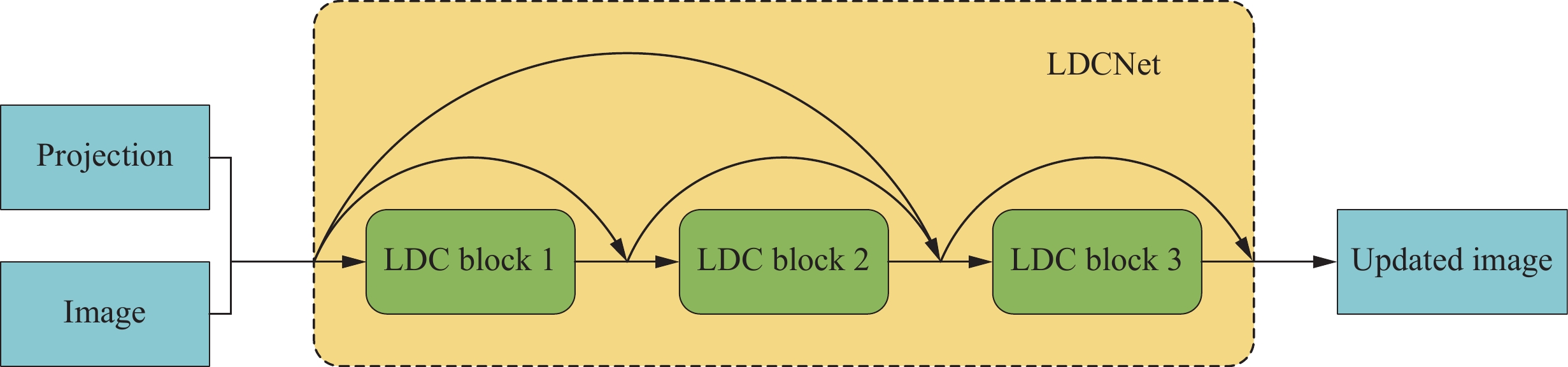
First, we introduce the LDC Block, which is the basic building unit of the data consistency processing module. When input data enters the LDC Block, the current reconstructed image and data consistency term are first concatenated along the channel dimension, allowing the network to simultaneously access both types of information. The concatenated data then passes through a feature extraction and transformation network, which begins with convolutional layers and processes features through residual blocks, channel attention, and spatial attention modules. This multi-level feature extraction and attention-enhanced design enables LDCNet to adaptively learn the weight distribution of data consistency. Figure 3 depicts the structure of LDC block.

Figure  3.  LDC Block Structure

下载: 全尺寸图片 幻灯片

Each LDC Block has its own weight parameter alpha and bias parameter beta, which are automatically adjusted during training to form a flexible dual-path regulation mechanism. The α parameter controls the influence of the data consistency term after processing through the feature network, while the β parameter acts directly on the original data consistency term, providing a linear bypass channel. This design enables the network to dynamically adjust its update strategy at each iteration step based on specific conditions. The computation is as follows:

Of particular note is the weight map generated by the network, which assigns a weight value between 0 and 1 to each pixel position, achieving spatial adaptability of data consistency constraints. This enables the network to learn to identify which regions require stronger data consistency constraints and which regions can be relatively relaxed, thereby effectively suppressing noise and artifacts while preserving important structures. The weight map is computed as follows:

First, compute the feature extraction network:

Then compute the attention-enhanced weight map:

where Res denotes the residual block operation, CA represents channel attention, SA represents spatial attention, and ⊙ denotes element-wise multiplication.

The learnable data consistency layer LDCNet serves as a high-level encapsulation of the entire module, containing multiple LDC Block instances that match the number of iterations. Each LDC Block corresponds to a specific iteration update, maintaining identical network architecture but with independent learnable parameters. During forward propagation, the network selects the appropriate LDC Block for processing based on the current iteration index. For example, at iteration t, the t-th LDC Block is activated to process the data. This design allows the network to adaptively adjust the strength of data consistency constraints at different iteration stages. The optimal number of iterations was determined through experimental validation, which is detailed in the discussion section. The structure of LDCNet is shown in Figure 4.

Figure  4.  LDCNet Structure

下载: 全尺寸图片 幻灯片

Additionally, LDCNet introduces global weight and bias parameters to regulate the intensity of data consistency constraints at a higher level. The global weight serves as a scaling factor that uniformly adjusts the intensity of data consistency updates across all iteration steps, while the global bias provides baseline adjustment for the data consistency term. These two global parameters are automatically learned through backpropagation, enabling the model to holistically adapt to different reconstruction tasks and data characteristics. The image update computation is as follows:

2.   Results

2.1   Dataset

This study utilizes the dataset provided by the DL-sparse-view CT competition in the AAPM Grand Challenge (https://www.aapm.org/GrandChallenge/DL-sparse-view-CT/). The dataset consists of 4000 training images with dimensions of 512×512 pixels, generated from breast phantom simulations, with an additional 10 images for testing. The simulation model features complex random structures within circular cross-sections, designed to simulate fibroglandular tissue in the breast. Each training image is accompanied by corresponding projection data (sinograms) acquired through 360-degree fan-beam projections with 128 views. Additionally, the dataset includes reconstructed images obtained using the FBP algorithm applied to these 128-view projection data.

2.2   Implementation Details

All experiments were conducted on a workstation equipped with an NVIDIA RTX 3090 GPU (24 GB memory), dual Jintide M88 JTMX08101 processors (16 cores 32 threads each at 2.1 GHz), 128 GB DDR4 RAM, running Ubuntu 22.04 LTS operating system.

For the training strategy, we adopted a multi-stage training approach, first pre-training the image enhancement subnetwork TIENet, followed by training the TransitNet. During the training process, we utilized the Adam optimizer with an initial learning rate of 1 e-3 and implemented a learning rate decay strategy. Due to computational resource constraints, the batch size was set to 2 and the epochs number was set to 100. To enhance the model’s generalization capability, we employed 10-fold cross-validation for data partitioning, training the model separately on each fold. The loss function incorporated MSE, along with supervision from multiple image quality assessment metrics including RMSE, PSNR, and SSIM.

For comparative experiments, we also employed 10-fold cross-validation, with batch sizes adjusted according to available computational resources, and the same number of epochs as used in training TransitNet.

2.3   Evaluation Metrics

To comprehensively evaluate the performance of reconstruction algorithms, this study employs three complementary image quality metrics: Root Mean Square Error (RMSE), Peak Signal-to-Noise Ratio (PSNR), and Structural Similarity Index (SSIM). The formulas for calculating RMSE, PSNR, SSIM are as follows:

where $ {x}_{ij} $ and $ \widehat{{x}_{ij}} $ represent the pixel values at position $ (i,j) $ in the reference image and reconstructed image respectively, and M and N denote the height and width of the image.

where $ MA{X}_{I} $ represents the maximum possible pixel value of the image (e.g., 255 for an 8-bit image), and MSE is the Mean Square Error.

where $ {\mathrm{\mu }}_{x} $ and $ {\mathrm{\mu }}_{y} $ are the means of images x and y respectively, $ {\mathrm{\sigma }}_{x}^{2} $ and $ {\mathrm{\sigma }}_{y}^{2} $ are the variances, $ {\mathrm{\sigma }}_{xy} $ is the covariance, and $ {c}_{1} $ and $ {c}_{2} $ are small constants to prevent division by zero.

2.4   Quantitative Results

This section compares the performance of different reconstruction algorithms on the AAPM dataset. The experiment evaluates several representative algorithms, including the traditionalFBP algorithm, deep learning-based FBPConvNet and RED-CNN, Transformer-based Uformer and SwinIR, iterative optimization-based TV and RTV methods, and our proposed TransitNet. To comprehensively assess the performance of each algorithm, the analysis was conducted from two dimensions: quantitative metrics and visual quality. The quantitative evaluation employs three complementary image quality metrics - RMSE, SSIM, and PSNR, while the visual quality analysis evaluates the reconstruction effectiveness of different algorithms by comparing the detail representation of reconstructed images.

As shown in Table 1, TransitNet exhibits superior performance across all quantitative metrics. Specifically, TransitNet achieves a PSNR of 45.8486 dB, which represents a substantial improvement of 19.0084 dB over the traditional FBP algorithm (26.8402 dB). In comparison with deep learning-based methods, TransitNet significantly outperforms RED-CNN (33.0535 dB), FBPConvNet (36.4081 dB), and more recent Transformer-based architectures including Uformer (38.1376 dB) and SwinIR (37.2184 dB). When compared to iterative optimization methods, TransitNet demonstrates superior performance with an RMSE of 0.0051, notably lower than both TV (0.0198) and RTV (0.0163). Furthermore, TransitNet achieves a higher PSNR (45.8486 dB vs 42.2334 dB) and SSIM (0.9590 vs 0.9018) compared to the baseline ItNet model, quantitatively validating the effectiveness of our proposed network enhancements.

Table  1.  Results of Various Reconstruction Algorithms

Algorithms	RMSE	PSNR	SSIM
FBP	0.0455	26.8402	0.6003
RED-CNN	0.0222	33.0535	0.8613
FBPConvNet	0.0151	36.4081	0.8922
SwinIR	0.0138	37.2184	0.9187
Uformer	0.0124	38.1376	0.9423
TV	0.0198	34.0534	0.9976
RTV	0.0163	35.7495	0.9983
ItNet	0.0077	42.2334	0.9018
TransitNet	0.0051	45.8486	0.9590

下载: 导出CSV 

| 显示表格

2.5   Visual Quality Results

Figure  5.  Results of Various Reconstruction Algorithms

下载: 全尺寸图片 幻灯片

Figure  6.  ROI in Results of Various Reconstruction Algorithms

下载: 全尺寸图片 幻灯片

From the visual quality comparison of reconstructed images, deep learning-based FBPConvNet and RED-CNN can suppress noise to some extent, but their detail preservation is less than ideal. Transformer-based Uformer and SwinIR show improvements in detail preservation, but still suffer from a certain degree of blurring. The iterative optimization-based TV and RTV methods achieve a good balance between artifacts suppression and detail preservation, though they show slightly insufficient edge sharpness. In contrast, our proposed TransitNet not only effectively suppresses artifacts but also excellently preserves image detail structures, producing reconstructed images that more closely resemble the reference images and demonstrating optimal visual reconstruction effects. Moreover, the images reconstructed by the FBP algorithm exhibited conspicuous artifacts and lacked reference value; therefore, the resultant image were not presented in the paper.

2.6   Ablation Studies

To validate the effectiveness of key modules in the proposed method, we conducted a series of ablation studies. First, we compared the performance of three different network architectures: using U-Net alone, using standard Transformer, and using linear attention mechanism, which verified the roles of the Transformer module and linear attention mechanism. Subsequently, by comparing fixed-weight and learnable-weight data consistency schemes, we validated the necessity of the learnable data consistency module.

2.6.1   Validating the Effects of Transformer Module and Linear Attention Mechanism

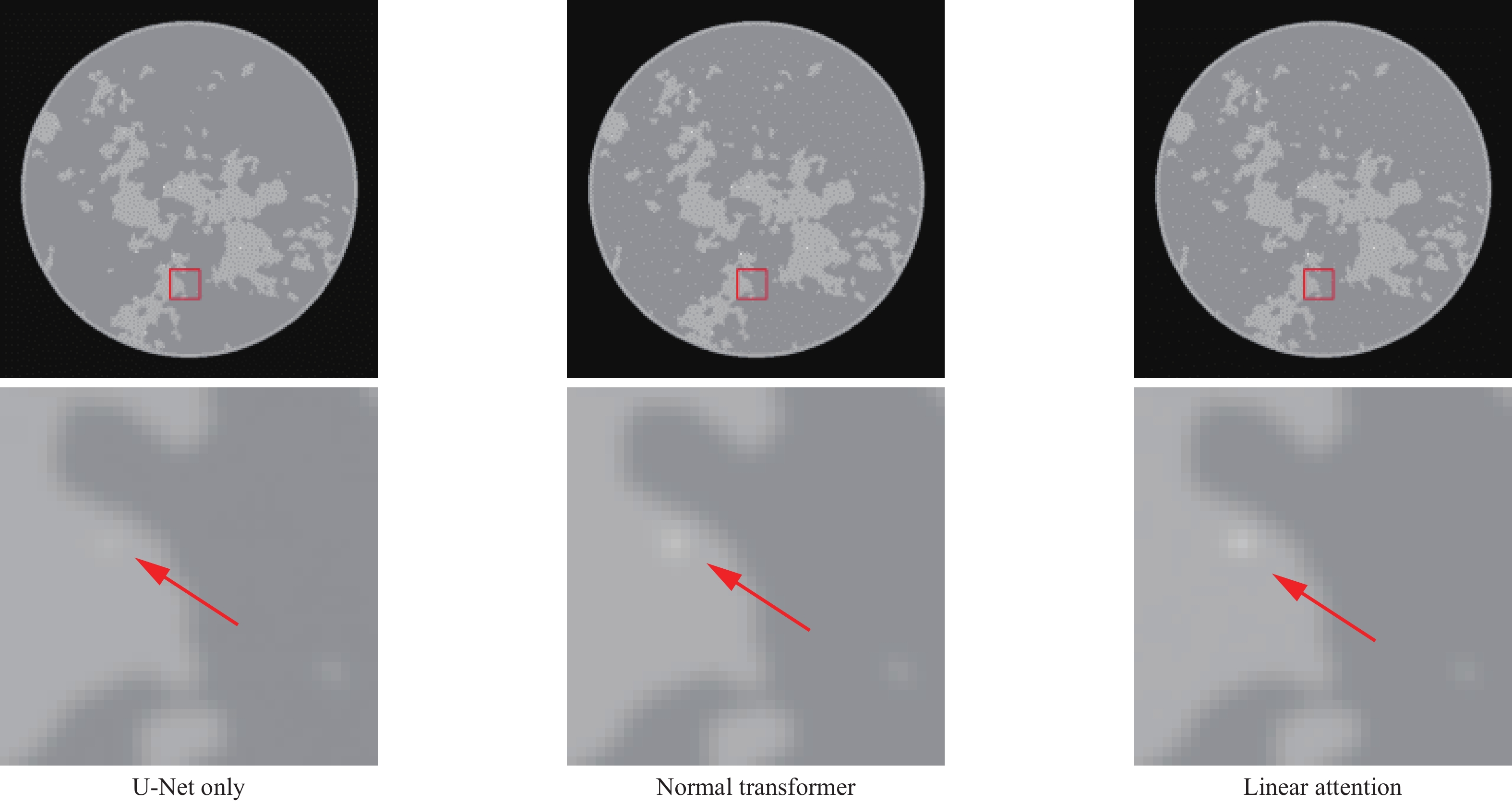
As shown in Table 2, incorporating the Transformer module enhances reconstruction performance, with the standard Transformer showing nearly 6 dB improvement in PSNR, 48% reduction in RMSE, and 0.1 increase in SSIM compared to using U-Net alone. However, the standard Transformer introduces substantial computational overhead, with parameter count increasing by 60% from 30 M to 48.3 M, FLOPs rising from 96.47 G to 178.94 G, memory consumption increases from 4.6 GB to 28.4 GB, training time grows from 7.2 h to 34.2 h. After implementing the linear attention mechanism, although there is a 1.8 dB decrease in PSNR compared to the standard Transformer, it still maintains a 4 dB advantage over U-Net while reducing FLOPs by 30% (from 178.94 G to 124.86 G), and parameter count by 18% (from 48.3 M to 39.6 M), memory usage by 53% (from 28.4 GB to 13.3 GB), and training time by 34% (from 34.2 h to 22.6 h). This indicates that the linear attention mechanism serves as an effective optimization strategy, maintaining most performance benefits while improving computational efficiency.

Table  2.  Results of Different Image Enhance Net

Image Enhance Net	Training Time∕min/epoch	#param.	FLOPs	Memory/GB	RMSE	PSNR	SSIM
U-Net Only	7.2	30 M	96.47 G	4.6	0.0079	42.2568	0.8636
Normal Transformer	34.2	48.3 M	178.94 G	28.4	0.0041	48.1445	0.9642
Transformer with Linear Attention	22.6	39.6 M	124.86 G	13.3	0.0051	45.8486	0.9590

下载: 导出CSV 

| 显示表格

Figure  7.  Results of Normal Transformer and Linear Attention Mechanism

下载: 全尺寸图片 幻灯片

Comparing the visual effects of reconstructed images, it is evident that using U-Net alone results in noticeable blurring and loss of details. After introducing the standard Transformer, image clarity and detail representation are improved, with sharper edges and more complete structural preservation. Although the linear attention mechanism scheme is slightly inferior to the standard Transformer in detail preservation, it still notably outperforms the pure U-Net architecture while reducing computational overhead while maintaining good reconstruction quality. These visual effects align with the trends observed in quantitative metrics, further validating the effectiveness of the Transformer module and linear attention mechanism. Overall, the linear attention scheme achieves the optimal balance between reconstruction quality and computational resource consumption, proving to be a practical improvement solution.

2.6.2   Validating the Effectiveness of Learnable Data Consistency

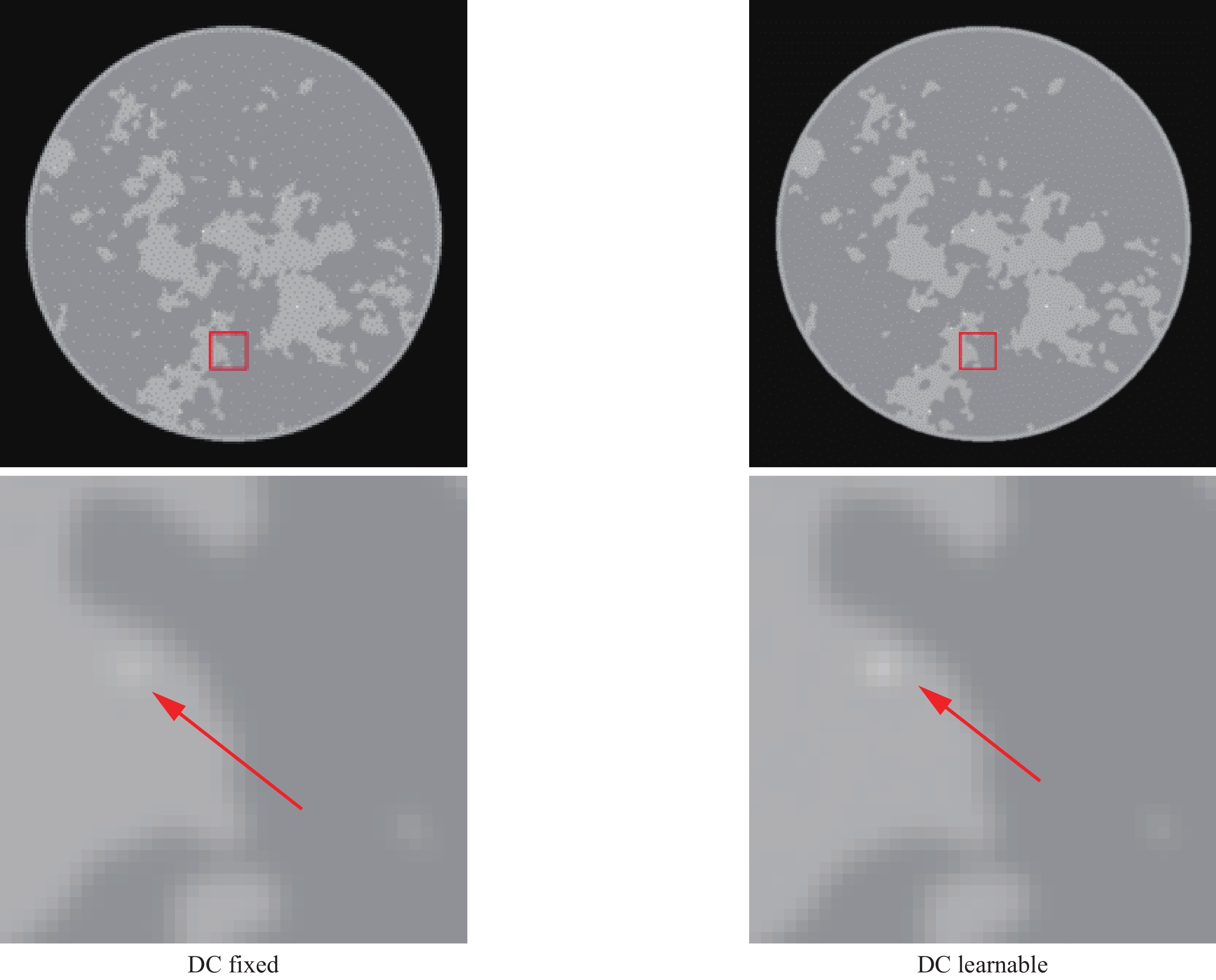
The data in Table 3 reveals that the learnable data consistency module achieves performance improvements compared to the fixed-weight approach. In terms of RMSE, the learnable scheme achieves 0.0051, representing a 24% reduction from the fixed-weight value of 0.0067. The SSIM increases from 0.9188 to 0.9590, showing an improvement of 0.04. The enhancement in PSNR is particularly notable, rising from 43.8670 dB to 45.8486 dB, demonstrating a substantial improvement of 2 dB.

Table  3.  Results of Fixed and Learnable Data Consistency

Data Consistency	RMSE	SSIM	PSNR
Fixed	0.0067	0.9188	43.8670
Learnable	0.0051	0.9590	45.8486

下载: 导出CSV 

| 显示表格

Figure  8.  Results with Fixed and Learnable Data Consistency

下载: 全尺寸图片 幻灯片

Comparison of reconstructed images reveals that the fixed-weight data consistency scheme produces images with noticeable blurring and artifacts. In contrast, the learnable weight approach not only better suppresses noise and artifacts but also better preserves image detail structures and edge features, resulting in clearer and more natural reconstructed images. These visual improvements align with the enhancement in quantitative metrics, further validating the effectiveness of the learnable data consistency module. The results from both aspects demonstrate that by learning learnable data consistency weights, the network can better balance the fidelity of measurement data and reconstruction image quality, thereby achieving superior reconstruction results.

3.   Discussion

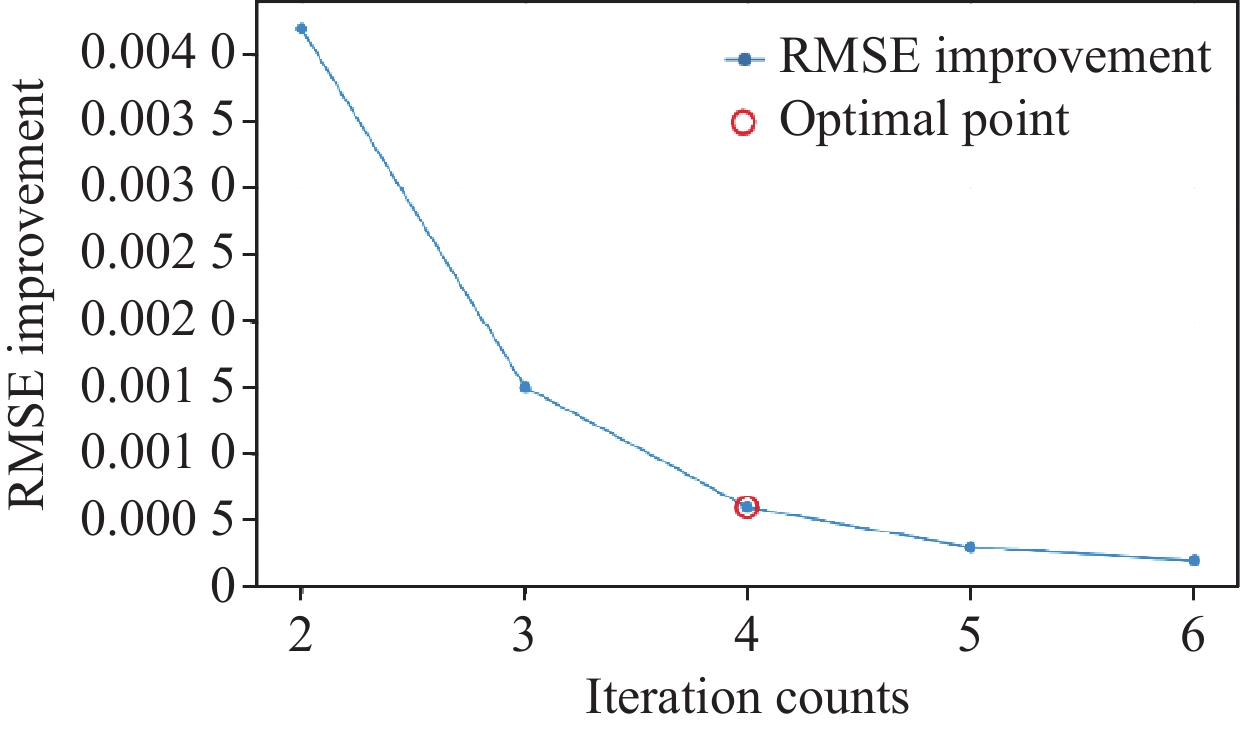
Table 4 demonstrates the variation of different evaluation metrics with respect to the iteration count. Figure 9 illustrates the improvement in reconstruction quality with each additional iteration. The analysis of iteration count’s impact on reconstruction performance reveals a consistent improvement trend in reconstruction quality as the number of iterations increases. With fewer iterations, each additional iteration brings notable performance enhancement, indicating that the network can progressively refine and optimize reconstruction results through multiple iterations. Specifically, when increasing the iteration count from 3 to 4, we observe a significant PSNR improvement of approximately 1 dB, while the improvement from 4 to 5 iterations yields only 0.5 dB gain. Moreover, the training time increases approximately linearly with the number of iterations. After reaching four iterations, the rate of performance improvement begins to plateau, suggesting that the network has essentially converged to a stable state. Although further increasing the iteration count still yields marginal performance improvements, considering the additional computational overhead and the diminishing returns in reconstruction quality, four iterations achieve an optimal balance between reconstruction quality and computational efficiency. This iterative convergence characteristic resembles traditional iterative reconstruction algorithms, demonstrating that the proposed deep learning framework inherits the advantageous properties of iterative reconstruction while accelerating convergence through learnable network modules. Furthermore, the continuous improvement in reconstruction quality indirectly validates the rationality of the network design, indicating that each iteration effectively extracts and utilizes image information.

Table  4.  Results with Different Iteration Counts

Iteration Counts	Training Time∕min/epoch	RMSE	SSIM	PSNR
1	11.2	0.0115	0.8387	38.7860
2	15.2	0.0072	0.8636	42.8534
3	18.8	0.0057	0.9341	44.8825
4	22.6	0.0051	0.9590	45.8486
5	26.3	0.0048	0.9715	46.3752
6	29.8	0.0046	0.9734	46.7448

下载: 导出CSV 

| 显示表格

Figure  9.  RMSE Improvement with Different Iteration Counts

下载: 全尺寸图片 幻灯片

4.   Conclusions

This paper presents TransitNet, an unrolling-based deep neural network for low-dose CT image reconstruction. The method organically combines physics model-driven data consistency constraints with deep learning’s feature extraction capabilities, achieving high-quality reconstruction through the introduction of Transformer mechanisms and learnable data consistency operations. Experimental results demonstrate that TransitNet achieves a good balance between reconstruction quality and computational efficiency. The incorporation of Transformer modules enhances reconstruction performance, while the linear attention mechanism effectively reduces computational overhead while maintaining most performance advantages. The learnable data consistency module enables better balance between measurement data fidelity and reconstruction image quality through adaptive weight adjustment. Experiments with iteration counts show that the network reaches a stable state after 4 iterations, demonstrating rapid convergence. Compared to existing methods, TransitNet not only effectively suppresses noise and artifacts but also well preserves image detail structures, showing excellent performance in both quantitative metrics and visual quality. These results indicate that combining deep learning with traditional reconstruction methods is a promising research direction, and the framework proposed in this paper provides an effective solution for this approach. Future work can further explore more efficient attention mechanisms and data consistency optimization strategies to further improve reconstruction performance and computational efficiency.