Rapid Exploration of Soil Strata in a Basin using Ground Penetrating Mirroring
-
摘要:
传统的地震反射方法，主要是利用来自波阻抗界面的反射波同相轴来刻画地质构造，据此获得地层界面、结构等信息。本研究提出利用反射波信息进行土壤层层速度快速反演的方法，将其命名为“地震反射探地镜”。该方法将反射信号自适应提取、均方根速度自动拾取和层速度快速反演相结合，形成一个用于近地表介质层速度快速探测和反演的探地镜方法。利用实测数据对该方法进行了评价，应用结果表明该方法能够快速提供地下介质的层速度和结构信息。在已知部分地质先验信息的情况下，可以将反演的层速度转换为土壤层的单轴抗压强度，为城镇的地基评价提供基础数据。
Abstract:In traditional seismic reflection exploration, geological structures are characterized only by interpreting reflection wave events from wave impedance interfaces and then obtaining information of stratigraphic interfaces and structures. Herein, we present a method used to rapidly invert velocities of seismic waves reflected from strata layers. We have named this method “Seismic Reflective Ground Penetrating Mirroring (SRGPM).” This method consists of three steps, which are: 1) adaptive extraction of respective reflection signals, 2) automatic selection of root mean square velocity, and 3) fast inversion of layer velocity. The validity of the proposed method was verified with field data. The layer velocities and structures of strata can be quickly acquired by SRGPM. Combining this data with prior geological information, the inverted layer velocities can be converted into the uniaxial compressive strengths of the soil layers, providing basic data for evaluation of urban foundations.
-
颈胸腹盆联合增强CT扫描是乳腺癌术前评估和术后复查最常用的影像检查手段之一[1]，对于淋巴结的检出，具有较高准确性、灵敏度和特异度[2]。随着CT设备发展更新[3-4]，能谱CT逐步应用于临床，它不仅可以提供常规影像资料，还可以提供多参数功能信息，因此受到临床的青睐[5]。但是能谱CT的辐射剂量往往等于或略高于同等图像质量下的常规CT扫描模式[3,6-8]。
本研究旨在探讨乳腺癌患者行颈胸腹盆联合增强CT常规和能谱两种扫描方案的技术要点，比较两种扫描模式的辐射剂量及图像质量，从而评价能谱CT对乳腺癌患者颈胸部淋巴结显示的应用价值。
1. 资料与方法
1.1 研究对象
回顾性分析我院2020年10月至2022年3月因乳腺癌行颈胸腹盆增强CT扫描患者的CT扫描资料，选取其中能谱CT扫描模式20例，常规非能谱模式CT扫描20例，年龄（56.65±11.79）岁。纳入标准：①女性；②选择颈胸腹盆 CT剂量指数（CT Dose Index，CTDvol）8＜CTDvol＜10范围内的患者。排除标准：①患者不能按扫描方案流程配合，导致图像伪影严重；②其他非扫描技术原因导致图像伪影严重的患者。
1.2 扫描前准备
患者检查前一周避免做胃肠道钡餐检查；前一天进行胃肠道准备，检查前禁食6～8 h，饮水充盈膀胱；去除假牙、项链等金属异物；扫描前服温水800～1000 mL充盈胃部[1]。
1.3 对比剂注射
选用20 G静脉留置针于右侧肘前静脉注穿刺，采用高压注射器团注对比剂碘海醇（含碘350 mgI/mL），对比剂注射时间均为25 s，按照如下公式计算对比剂剂量和流率：
$$ \begin{aligned} 对比剂总量（{\text{mL}}） =体重（{\text{kg}}） {\text{×1.17}}\;{\text{mL}}/{\text{kg}}，\\ 流率（{\text{mL}}/{\text{s}}） =对比剂总量（{\text{mL}}） /{\text{25}}\;{\text{s}}，\;\;\;\end{aligned} $$ 对比剂注射完毕以相同速率追加盐水30 mL。
1.4 CT扫描参数
常规CT扫描。采用GE（GE Discovery CT750 HD）CT行颈胸腹盆 Ⅲ期常规联合扫描，扫描流程如表1。患者仰卧位，足先进，扫描方向头-足。扫描参数：采用螺旋Helical方式扫描，探测器准直宽度40 mm，球管转速0.6 s/r，螺距0.984︰1，层厚5 mm；重建间隔5 mm。管电压120 kV，管电流采用智能管电流技术（Smart mA=200～600 mA）。采用对比剂追踪技术，监测胸降主动脉层面，触发阈值达到200 HU后启动动脉期扫描，采集 Ⅲ 期常规增强图像。
表 1 常规颈胸腹盆增强CT扫描流程Table 1. Conventional scanning process of neck-chest-abdomen-pelvis combined enhanced CT项目 扫描启时间/s 患者姿势 扫描范围 胸腹盆动脉期 25～30 上举双手在头颅两侧 肺尖至耻骨联合 颈部动脉期 40 放手在身体两侧 胸锁关节至乳突 胸腹盆静脉期 60 上举双手在头颅两侧 肺尖至耻骨联合 腹盆延时期 180 上举双手在头颅两侧 肝顶至耻骨联合 能谱CT扫描。采用GE（GE Revolution）CT行颈胸腹盆 Ⅲ 期能谱扫描，扫描流程如表2。患者仰卧位，足先进，扫描方向头-足。扫描参数：探测器宽度80 mm，球管旋转时间0.8 s/r，螺距0.992︰1，层厚5 mm，重建间隔5 mm；A、B球管管电压分别为80 kV和140 kV，管电流275 mAs，管电流模式GSI Assist。扫描后自动生成单能量120 keV图像。采用对比剂追踪技术，监测胸降主动脉层面，触发阈值达到200 HU后启动动脉期扫描，采集 Ⅲ 期能谱CT图像。
表 2 能谱颈胸腹盆增强CT扫描流程Table 2. Dual-energy scanning process of neck-chest-abdomen-pelvis combined enhanced CT项目 扫描启动时间/s 患者姿势 扫描范围 颈胸腹盆动脉期 25～30 上举双手在头颅两侧 乳突至耻骨联合 颈胸腹盆静脉期 60 上举双手在头颅两侧 乳突至耻骨联合 腹盆延时期 180 上举双手在头颅两侧 肝顶至耻骨联合 上述常规CT扫描及能谱CT扫描模式中，在动脉期及延迟期两种扫描模式具有相同的扫描范围，即动脉期扫描范围颈胸腹盆，延迟期腹盆，所以选取动脉期及延迟期用以比较两种扫描方式的辐射计量差别。选取常规CT动脉期颈胸部图像和能谱CT动脉期颈胸部单能量120 keV图像来进行图像质量评价，其他图像不作为本次研究使用。
1.5 辐射剂量统计
记录检查结束后CT机自动生成的辐射剂量报告数据，CT计量指数和计量长度乘积（dose length product，DLP），并计算有效剂量（effective radiation dose，ED）的计算公式E=k×DLP，式中k的单位为mSv[9]，颈部、胸部、腹盆部k值分别取0.0059、0.014和0.015。
1.6 图像质量评价
1.6.1 客观图像质量评价
测量颈部淋巴结和腋窝淋巴结的CT平均值（以下简称CT值）及标准误值（standard deviation，SD），测量感兴趣区（region of interest，ROI）设为圆形，选取最大淋巴结显示层面；选取同层面颈部的皮下脂肪，并测量其CT平均值及SD值。计算其信号噪声比（signal-to-noise ratio，SNR）、对比噪声比（contrast-to-noise ratio，CNR）。
SNR=CT淋巴结/SD淋巴结，
CNR=（CT淋巴结 - CT脂肪）/SD脂肪。
1.6.2 主观图像质量评价
由两名从事影像诊断3年和5年的放射科医师对颈部胸部图像进行主观分析，意见不统一时，由另一名从事影像诊断20年的放射科医师仲裁，并确定最终意见。对图像的总体图像质量进行主观评分，采用5级评分法[7]，3分及以上满足诊断要求。
1分：无法诊断，图像整体受线性硬化束伪影影响严重，图像质量差，无法区分淋巴结与其他组织。2分：影响诊断，图像整体受线性硬化束伪影影响较大，图像质量较差，可以区分淋巴结与其他组织。3分：可以诊断，图像局部受线性硬化束伪影影响较大，图像质量一般，淋巴结，大小、形态、数量显示明确。4分：明确诊断，图像局部受线性硬化束伪影影响轻微，图像质量良好，淋巴结大小、形态、数量显示清晰。5分：明确诊断，图像无线性硬化数伪影影响，图像质量优秀，淋巴结大小、形态、数量显示清晰。
1.7 统计学分析
本研究采用SPSS 26.0进行统计学分析。首先对相关数据行正态性检验，若符合正态分布，则以
$\bar x \pm s $ 表示，通过单因素方差分析比较常规和能谱CT颈胸腹盆动脉期和延时期辐射剂量CTDvol值、DLP值、ED的组间差异以及常规和能谱CT动脉期颈和胸部淋巴结CT值、SD值、SNR值、CNR值和同层面脂肪的CT值、SD值的组间差异，并行邦弗伦尼检验比较组内差异；若为偏态数据，以M（Q1，Q3）表示，通过Kruskal-Wallis U检验比较其差异性。此外，对于常规和能谱CT动脉期的颈部和胸部淋巴结图像的主观质量评价，通过kappa检验评价观察者间的一致性：Kappa值≤0.40为一致性较差，0.40＜Kappa值≤0.75为一致性中等，Kappa值＞0.75为一致性较好。采用Kruskal-Wallis U检验比较常规和能谱CT动脉期的颈部和胸部淋巴结图像两组图像质量的差异性。P＜0.05表示存在统计学差异。
2. 结果
2.1 辐射剂量比较
常规和能谱颈胸腹盆联合增强CT扫描方案的动脉期和延迟期CTD值、DLP值及ED值，具有统计学差异，且能谱低于常规CT扫描方案的辐射剂量（表3）。
表 3 常规和能谱颈胸腹盆联合增强CT扫描方案动脉期和延时期辐射剂量统计表Table 3. Statistical table of radiation dose in arterial phase and extended phase of conventional and dual-energy scanning process of neck-chest-abdomen-pelvis combined enhanced CT项目 指标 辐射剂量 统计检验 常规 能谱 统计值 P 动脉期 DLP 804.84±67.12 676.62±87.02 -5.218 <0.001 CTDvol 9.40±0.60 8.33±0.79 -4.851 <0.001 ED 12.07±1.01 10.15±1.31 -5.218 <0.001 延迟期 DLP 378.48±80.64 307.80±16.44 -3.841 0.001 CTDvol 8.14±1.37 6.25±0.26 -6.038 <0.001 ED 5.68±1.21 4.62±0.25 -3.841 0.001 2.2 客观图像质量评价
常规和能谱颈胸腹盆增强CT扫描方案之间比较，颈部动脉期淋巴结的CT平均值、SD值、SNR值、CNR值以及同层面的脂肪CT值和SD值均不存在统计学差异（表4）。常规和能谱颈胸腹盆增强CT扫描方案之间比较，胸部动脉期腋窝淋巴结的CT值和同层面的脂肪CT值均不存在统计学差异，腋窝淋巴结常规和能谱扫描的SD值、SNR值、CNR值存在统计学差异（表4）。
表 4 常规和能谱颈胸腹盆联合增强CT扫描方案动脉期颈部和胸部淋巴结客观图像质量评价表Table 4. Evaluation table of objective image quality of cervical and thoracic lymph nodes in arterial phase in conventional and dual-energy scanning process of neck-chest-abdomen-pelvis combined enhanced CT指标 项目 客观图像质量 统计检验 常规 能谱 统计值 P CT值 颈部淋巴结 52.47±13.03 45.29±9.58 -1.985 0.055 颈部同层面脂肪 -101.58±4.96 -100.27±5.26 -0.813 0.421 胸部淋巴结 36.92±16.09 39.35±15.94 0.480 0.634 胸部同层面脂肪 -106.72±8.46 -103.84±5.36 1.288 0.206 SD 颈部淋巴结 10.58±2.46 9.65±2.40 -1.206 0.235 颈部同层面脂肪 6.83±2.22 6.55±1.51 -0.463 0.647 胸部淋巴结 36.92±16.09 39.35±15.94 -4.871 0.001 胸部同层面脂肪 9.15±1.79 6.96±1.06 -4.722 ＜0.001 SNR 颈部淋巴结 5.26±1.99 5.12±2.12 -0.217 0.830 胸部淋巴结 2.88±1.48 4.32±1.84 2.726 0.010 CNR 颈部淋巴结 25.02±8.57 23.20±4.96 -0.825 0.416 胸部淋巴结 16.27±3.84 20.99±3.63 3.996 ＜0.001 2.3 主观图像质量评价
常规和能谱颈胸腹盆增强CT扫描方案颈部和胸部动脉期淋巴结的主观图像质量均满足临床诊断要求，两医师间主观评分一致性较好，颈部动脉期淋巴结图像质量的主观评分的Kappa值为0.792；胸部动脉期淋巴结图像质量的主观评分一致性0.916（表5）。
表 5 常规和能谱颈胸腹盆联合增强CT扫描方案主观图像质量评分表Table 5. Subjective image quality evaluation table of conventional and dual-energy scanning process of neck-chest-abdomen-pelvis combined enhanced CT项目 主观评分者 主观图像质量 统计检验 3分 4分 5分 Z P 颈部 观察者1 6 13 21 -0.763 0.495 观察者2 7 12 21 -0.596 0.602 胸部 观察者1 9 22 9 -3.724 0.001 观察者2 8 22 10 -3.756 ＜0.001 常规和能谱颈胸腹盆增强CT扫描方案比较，颈部动脉期淋巴结的主观图像质量评分，未见明确统计学差异；胸部动脉期淋巴结的主观图像质量评分，存在明显的统计学差异；能谱颈胸腹盆增强CT扫描方案的胸部主观图像质量优于常规的CT扫描方案的胸部主观图像质量。
3. 讨论
由于电离辐射存在诱发肿瘤的潜在风险，因此在获得满足诊断水平的图像的同时，如何尽可能地降低CT的辐射剂量，国内外学者做了很多研究，将CT的辐射剂量控制在满足诊断图像诊断的最低范围内，降低对电离辐射敏感的表浅器官晶状体、甲状腺、乳腺等损害的风险[10-11]。很多学者致力于使用能谱CT扫描来降低辐射剂量，展开了相关方面的研究[12-13]。
本研究通过比较常规和能谱颈胸腹盆增强CT扫描方案，动脉期和延时期的辐射剂量的比较发现，能谱颈胸腹盆扫描方案的辐射剂量更低，与文献一致[3,14-15]。动脉期常规和能谱颈胸腹盆增强CT扫描方案中颈部淋巴结客观和主观图像质量相同，但是能谱扫描的流程更加简单，患者更容易配合，目前国内外针对扫描流程简化的文献较少，亟待相关研究的展开；动脉期能谱颈胸腹盆增强CT扫描方案比常规胸部淋巴结客观和主观图像质量扫描更好，与文献一致[16]。
CT的射束硬化伪影是因为传统X线是混合能量射线，在穿过高能量的物质，低能射线容易被物质吸收衰减，而导致X线束的平均能量升高，产生线束硬化。例如对比剂、骨骼会导致周围组织的产生高低不均的条纹状伪影，干扰临近结构的显示，使得图像质量降低[17]。双臂上举对颈部常规增强CT检查产生射束硬化伪影对颈部周围软组织的图像质量产生影响，增强CT检查腋静脉和锁骨下静脉内的高浓度对比剂对腋下的软组织的图像质量同样产生影响，进而影响乳腺癌颈胸部淋巴结的显示和诊断。
因此本研究在常规颈胸腹盆增强CT扫描方案中，需要上举双臂至颈部两侧行胸腹盆动脉期扫描，之后需要患者配合技术员口令，迅速将上举双臂放于胸前，行颈部动脉期扫描，之后将手臂上举至头颅两侧进行胸腹盆静脉期扫描，以避免双臂对颈部图像质量的影响，但是对于腋静脉和锁骨下静脉的高浓度对比剂对周围软组织图像质量的影响无法去除。
能谱CT可实现40～140 keV能量范围内任意能量点的单能量图像提取。单能量图像理论上可以模拟单色X线光源下物体的成像，所以能够克服传统CT上经常出现的硬化伪影，其图像质量及对伪影区结构的显示明显优于常规混合能量图像[18]。最佳单能量点的选取可达到优化成像条件、消除硬化伪影、增加图像对比度的目的，本研究选取120 keV的单能量图像与文献一致[16]。
本研究的能谱颈胸腹盆增强CT扫描方案简化扫描流程，Ⅲ 期增强始终保持上举双臂至颈部两侧，通过能谱扫描产生的120 keV能谱单能量的颈部和胸部动脉期图像与常规图像的客观和主观图像质量比较，获得两种扫描方案的诊断效能相同。能谱扫描可以基本消除颈部因双臂上举带来的射束硬化伪影的影响（图1（a）和图1（b））。并且可以去除腋静脉和锁骨下静脉的高浓度对比剂对周围软组织图像质量的影响，更有利于对于乳腺癌颈胸部淋巴结的诊断（图1（c）和图1（d））。
![]()
图 1 常规和能谱颈胸腹盆联合增强CT颈部和胸部淋巴结图像（a）常规颈胸腹盆联合增强CT颈部淋巴结图像；（b）能谱颈胸腹盆联合增强CT颈部淋巴结图像；（c）常规颈胸腹盆联合增强CT胸部淋巴结图像，静脉中对比剂对淋巴结的显示产生影响；（d）能谱颈胸腹盆联合增强CT胸部淋巴结图像，基本去除静脉中对比剂对周围软组织的影响，腋窝淋巴结可以清晰显示。Figure 1. Cervical and axillary lymph nodes images of conventional and dual-energy scanning process of neck-chest-abdomen-pelvis combined enhanced CT能谱颈胸腹盆扫描方案操作更加简便，患者更容易配合，检查成功率高；不容易出现因患者乳腺癌术后淋巴回流不畅，大臂肿胀导致举放手缓慢，或因紧张听不清指令等配合不佳的情况，无法完成举放手配合，使得颈部出现射束硬化伪影，甚至出现运动伪影，导致检查图像质量下降，进而影响疾病的诊断。
另外能谱成像的多参数成像，除了可以提供40～140 keV能量范围内任意能量点的单能量图像，还可以根据能谱曲线计算得出病变组织的有效原子序数，以及基物质密度与其分布图像[19]。林桐[20]研究显示，对动脉期和静脉期碘基质浓度和分析能谱曲线特征的斜率比较，区分乳腺癌腋窝淋巴结转移情况。
本研究的局限性：①样本量有限，有待于大样本量的进一步验证；②理论上在同一患者行常规 CT及能谱CT更能准确比较剂量，但实施困难，所以本研究选取了颈胸腹盆增强CT扫描方案中动脉期颈胸腹盆的CT计量指数在同一范围内的患者来进行辐射剂量比较以期尽量提高结果的可靠性。
综上所述，能谱颈胸腹盆联合增强CT扫描方案的辐射剂量更低，扫描流程更简便，患者配合度更高，对于胸部淋巴结的显示更清晰，并且能谱扫描可以提供多参数的图像数据，具有重要的应用推广价值。
-
![]()
图 6 反演的房速度与钻孔资料对比图
Figure 6. Comparison of inverted interval velocity with drilling data
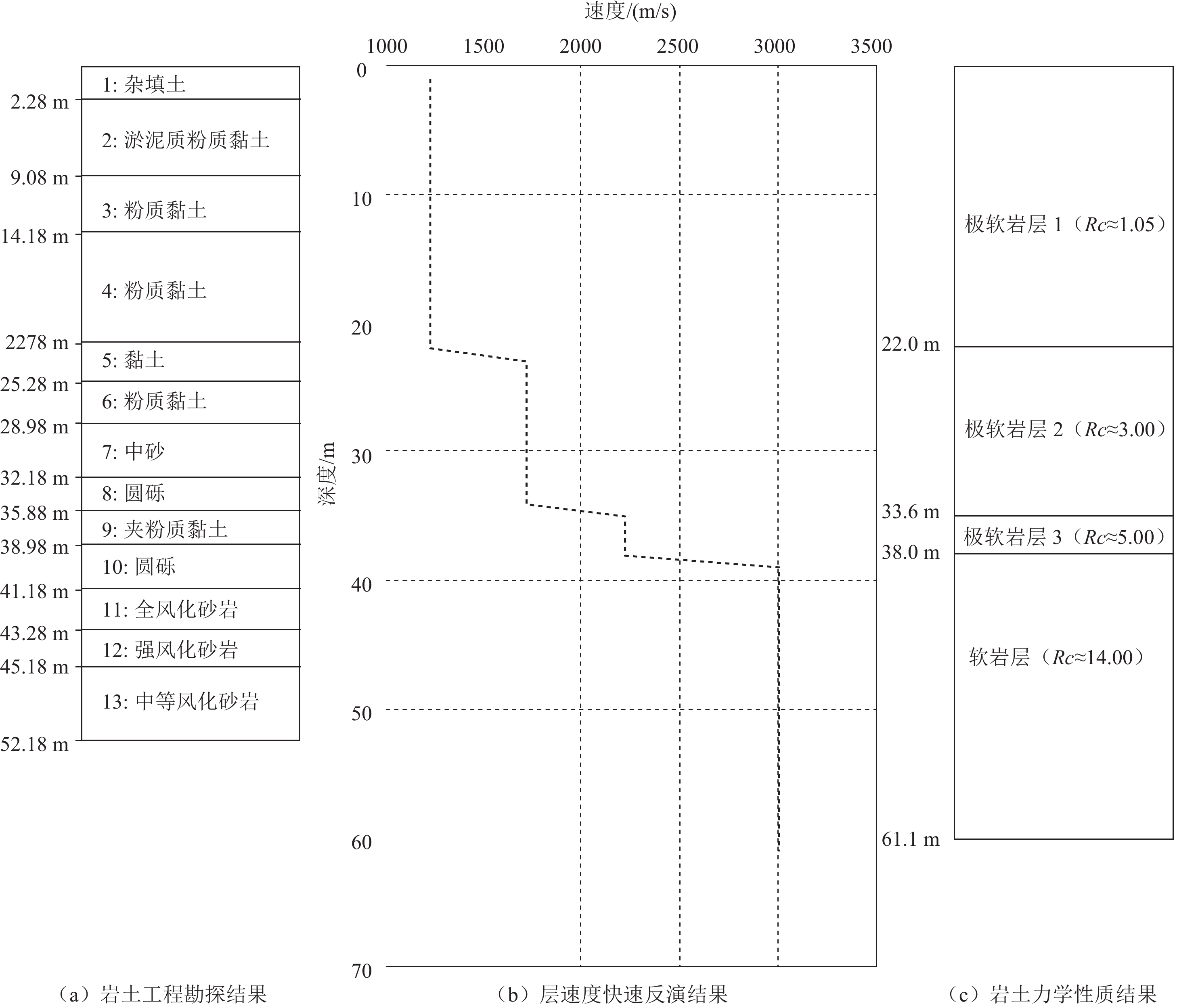
表 1 地下介质的速度、密度和泊松比参数
Table 1 Velocity, density, and Poisson’s ratio of subsurface materials
纵波速度/（m/s） 密度/（g/cm3） 泊松比 第1层 1224.5 1.8 0.4 第2层 1716.5 1.9 0.35 第3层 2215.5 1.9 0.35 第4层 3005.4 2.0 0.25 
下载: 导出CSV
表 2 岩石坚硬程度划分
Table 2 Rock category based on degree of hardness
岩石坚硬程度 岩石饱和单轴抗压
强度$ {R}_{c} $（MPa）硬质岩 坚硬岩 $ > 60 $ 较坚硬岩 $ 60~30 $ 软质岩 较软岩 $ 30~15 $ 软岩 $ 15~5 $ 极软岩 $ \le 5 $
下载: 导出CSV
-
[1] 魏雨浓, 石战结, 余天祥. 不同电极阵列联合反演在古墓探测中的应用[J]. CT理论与应用研究, 2022, 31(3): 280-292. DOI: 10.15953/j.ctta.2022.008. WEI Y N, SHI Z J, YU T X. Application of joint inversion of different electrode arrays in ancient mausoleum detection[J]. CT Theory and Applications, 2022, 31(3): 280-292. DOI: 10.15953/j.ctta.2022.008.
[2] 刘江平, 王莹莹, 刘震. 近地表反射和折射法的进展及应用[J]. 地球物理学报, 2015, 58(9): 3286-3305. Liu J P, Wang Y Y, Liu Z. Progress and application of near-surface reflection and refraction method [J]. Chinese J Geophys, 58(9): 3286-3305. (in Chinese).
[3] 韦红, 白清云, 孙佳林, 等. 地震信号谐波提频技术在辫状河砂体精细识别的应用[J]. CT理论与应用研究(中英文), 2024, 33(5): 577-584. DOI: 10.15953/j.ctta.2023.176. WEI H, BAI Q Y, SUN J L, et al. Application of Seismic Signal Harmonic Frequency Enhancement Technology for Fine Identification of Braided River Sand Bodies[J]. CT Theory and Applications, 2024, 33(5): 577-584. DOI: 10.15953/j.ctta.2023.176.
[4] 刘庆文, 秦德文, 胡伟. AVO 信息约束匹配追踪技术在富煤储层刻画中的应用[J]. CT理论与应用研究, 2023, 32(2): 189-197. DOI: 10.15953/j.ctta.2022.218. LIU Q W, QIN D W, HU W. Application of AVO Information-constrained Matching Pursuit Technique in Rich Coal Reservoir Characterization[J]. CT Theory and Applications, 2023, 32(2): 189-197. DOI: 10.15953/j.ctta.2022.218.
[5] MALEHMIR A, ZHANG F, DEHGHANNEJAD M, et al. Planning of urban underground infrastructure using a broadband seismic landstreamer—Tomography results and uncertainty quantifications from a case study in southwestern Sweden[J]. Geophysics, 2015, 80(6): B177-B192. DOI: 10.1190/geo2015-0052.1.
[6] MARTÍ D, CARBONELL R, FLECHA I, et al. High-resolution seismic characterization in an urban area: Subway tunnel construction in Barcelona, Spain[J]. Geophysics, 2008, 73(2): B41-B50. DOI: 10.1190/1.2832626.
[7] AHOKANGAS E, MÄKINEN J, ARTIMO A, et al. Interlobate esker aquifer characterization by high resolution seismic reflection method with landstreamer in SW Finland[J]. Journal of Applied Geophysics, 2020, 177: 104014. DOI: 10.1016/j.jappgeo.2020.104014.
[8] INAZAKI, TOMIO, 张弋. 应用于岩土力学的浅层反射地震[C]//勘探地球物理国际讨论会论文摘要, 北京, 1989. Inazaki T, Zhang G. Shallow reflection seismic method applied to geotechnical mechanics [C]//Proceedings of the International Symposium on Exploration Geophysics, Beijing, 1989.
[9] 周洪福, 聂德新, 王春山. 水电工程坝基玄武岩体波速与变形模量关系[J]. 地球科学(中国地质大学学报), 2015, 40(11): 1904-1912. ZHOU H F, NIE D X, WANG C S. Correlation between wave velocity and deformation modulus of basalt masses as dam foundation in hydropower projects[J]. Earth Science, 2015, 40(11): 1904-1912.
[10] 李文, 谭卓英. 基于P波模量的岩石单轴抗压强度预测[J]. 岩土力学, 2016, 37(S2): 381-387. LI W, TAN Z Y. Prediction of uniaxial compressive strength of rock based on P-wave modulus[J]. Rock and Soil Mechanics, 2016, 37(S2): 381-387.
[11] 张宜虎, 周火明, 邬爱清. 基于质量分级的岩体变形模量统计[J]. 岩石力学与工程学报, 2011, 30(3): 486-492. ZHANG Y H, ZHOU H M, WU A Q. Statistical analysis of deformation moduli of rock masses based on quality classification[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 486-492.
[12] JIANG J, YANG W, REN H. Seismic wavefield information extraction method based on adaptive local singular value decomposition[J]. Journal of Applied Geophysics, 2023, 210: 104965. DOI: 10.1016/j.jappgeo.2023.104965.
[13] YILMAZ O. Seismic Data Analysis[M]. Tulsa: Society of Exploration Geophysicists, 2001.
[14] ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd ACM International Conference on Knowledge Discovery and Data Mining (KDD), 1996, 226-231.
[15] 杨文采. 地球物理反演的理论与方法[M]. 北京: 地质出版社, 1997. YANG W C. Geophysical inversion theory and method [M]. Geology Press Beijing China, 1997.
[16] 张亚天. 浙江大学紫金港校区主干道路及校门建设工程岩土工程勘察报告[R]. 浙江城建勘察研究院有限公司, 2018. ZHANG Y T. Geotechnical Investigation Report on the Main Road and Gate Construction Project of Zijingang Campus in Zhejiang University [R]. Zhejiang Urban Construction Survey and Research Institute Co. , Ltd, 2018.
[17] 杨文采. 反射地震学理论纲要[M]. 北京: 石油工业出版社, 2012. YANG W C. Theoretical Outline of Reflection Seismology [M]. Petroleum Industry Press Beijing China, 2012.
[18] 中华人民共和国水利部. GB/T 50218-2014 工程岩体分级标准[S]. 北京: 中国计划出版社, 2014. Ministry of Water Resources of the PRC. GB/T 50218-2014 Standard for engineering classification of rock masses [S]. Planning Press Beijing China, 2014.
-
期刊类型引用(1)
1. 王诗耕，浦仁旺，刘义军，方鑫，魏巍，李贝贝. 能谱CT下肢静脉成像优化：模体研究. CT理论与应用研究(中英文). 2025(01): 73-81 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 37
- HTML全文浏览量: 6
- PDF下载量: 2
- 被引次数: 1
