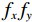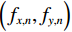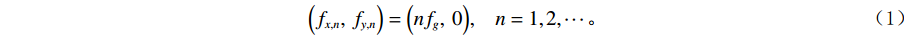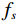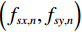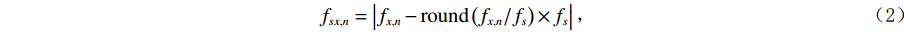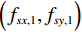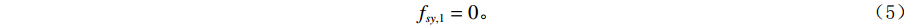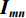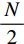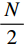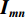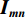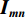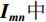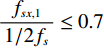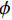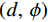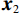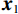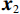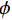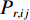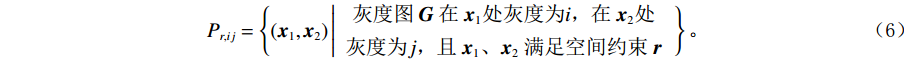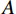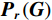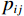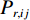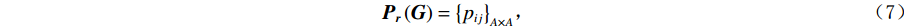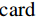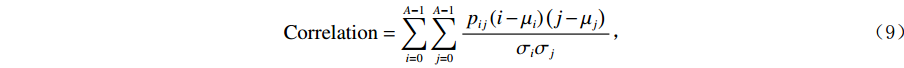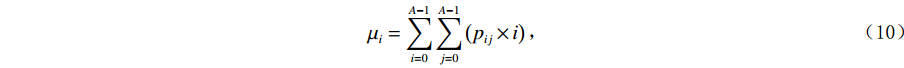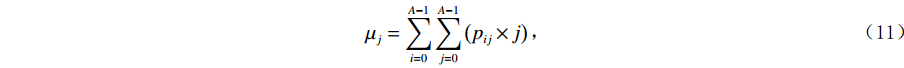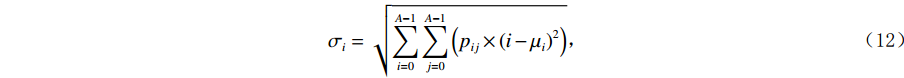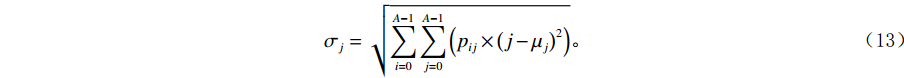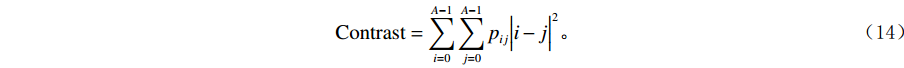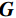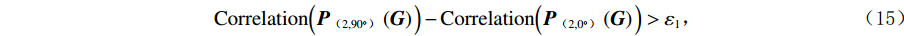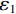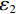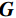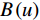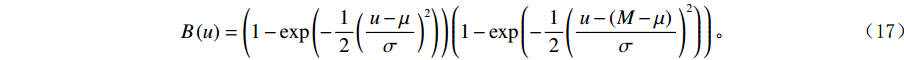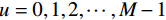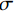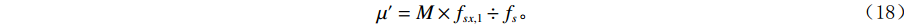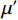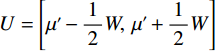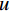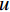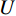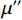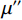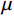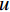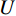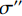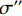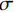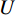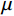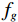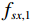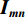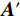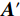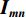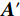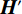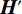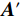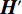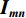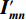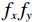Removal of Gridline Artifacts in Cone-beam CT Based on Wavelet Transform
-
摘要: 采用平板探测器的X射线锥束成像系统中,由于散射会带来图像伪影从而劣化图像质量,通常采用在平板探测器前安装滤线栅来去除散射,但滤线栅会在获取的图像上形成周期性的条状伪影,如何去除条状伪影是X射线锥束成像系统中的一个关键技术问题。本文对已有的滤线栅条纹去除方法进行概述,创新性地提出基于频谱拼接的小波变换方法,既能在损失物体细节信息少的前提下很好地去除滤线栅条纹,又不会引入小波变换谐波。通过实际实验,检验该方法的有效性。Abstract: In cone-beam computed tomography with flat-panel imagers, scattered X-ray photons lead to reduced image quality. Insertion of an anti-scatter grid between the patient or object and the flat-panel imagers is one of the most used techniques for reducing scattered radiation. However, while the scatter is reduced, gridline artifacts can be visible. Suppressing gridline artifacts in cone-beam computed tomography is significant. In this paper, the existing methods of removing gridline artifacts are summarized. Moreover, the wavelet transform method based on spectrum coalescence is innovatively proposed for removing gridline artifacts. Wavelet transform can remove gridline artifacts effectively and without introducing wavelet transform harmonics thus reducing the loss of object details. The effectiveness of this method is verified by experiments.
-
Keywords:
- gridline artifacts /
- wavelet transform /
- spectrum coalescence
-
计算机断层成像技术(computed tomography,CT),是20世纪医学诊断领域的重大成就。第一台临床计算机断层成像扫描装置诞生于1971年[1]。几十年来,CT技术的扫描方式发生了翻天覆地的变化,从单射线源、单探测器的平移旋转扫描,到多排探测器的多层螺旋扫描,数据采集速度不断加快,成像质量不断提高,CT技术得到了长足的发展。
近年来,采用平板探测器的锥束CT在口腔医学[2]、工业无损检测[3]等领域应用广泛。Feldkamp等[4]于1983年提出的FDK重建算法是锥束CT的理论基础。锥束CT具有数据射线利用率高、辐射剂量低等先天优势,但其由于锥角大,散射问题颇为严重。在平板探测器上叠放防散射滤线栅(anti-scatter grid),可以从根本上降低散射光子到达平板探测器的概率,从而减弱散射光子对CT重建图像质量的影响,但同时会引入滤线栅条纹。滤线栅条纹若不加以去除,CT重建图像中会出现明显的环状伪影。由于射束硬化、剩余散射等原因,直接增益校正通常不足以除尽滤线栅条纹,因而需要特殊的滤线栅条纹去除方法[5-6]。
滤线栅条纹去除方法,通常可分为空间域方法、频域滤波方法[7-8]、小波域抑制方法[9] 3类。空间域方法的代表是核函数卷积法,通过将含有滤线栅条纹的图像与核函数(比如高斯核)进行卷积,使滤线栅条纹模糊化;一般来讲,这类方法在去除滤线栅条纹的同时,物体的细节会变得模糊,即会损失较多的物体的高频信息。频域滤波法通常利用带阻滤波器,去除含有滤线栅条纹的图像在滤线栅条纹尖峰频率附近的频率成分,从而除去滤线栅条纹;一般来讲,相较于空间域方法,频域滤波法可以更好地抑制滤线栅条纹,且可保留更多的物体的细节信息,但使用该方法的前提是滤线栅条纹的频域分布不能和图像中有效信息的频域分布重叠。小波域抑制方法的初衷是进一步保留物体的细节信息,其通过逐层小波变换将含有滤线栅条纹的图像分解成一系列子图,并只对那些含有滤线栅条纹的子图做适当处理,以除去滤线栅条纹。原始的小波域抑制方法,直接将含有滤线栅条纹的子图的全部像素设为0,损失的物体细节较多,Tang[9]对这一方法做出了改进,用频域滤波的方法去处理那些含有滤线栅条纹的子图,更好地保留了物体的细节信息,但这一处理方法引入了小波变换谐波[10]。
本文创新性地提出基于频谱拼接的小波变换方法,既能在损失物体细节信息很少的前提下很好地抑制滤线栅条纹,又能避免小波变换谐波的产生。通过实际实验,验证这一方法的有效性。
1. 滤线栅条纹的物理建模
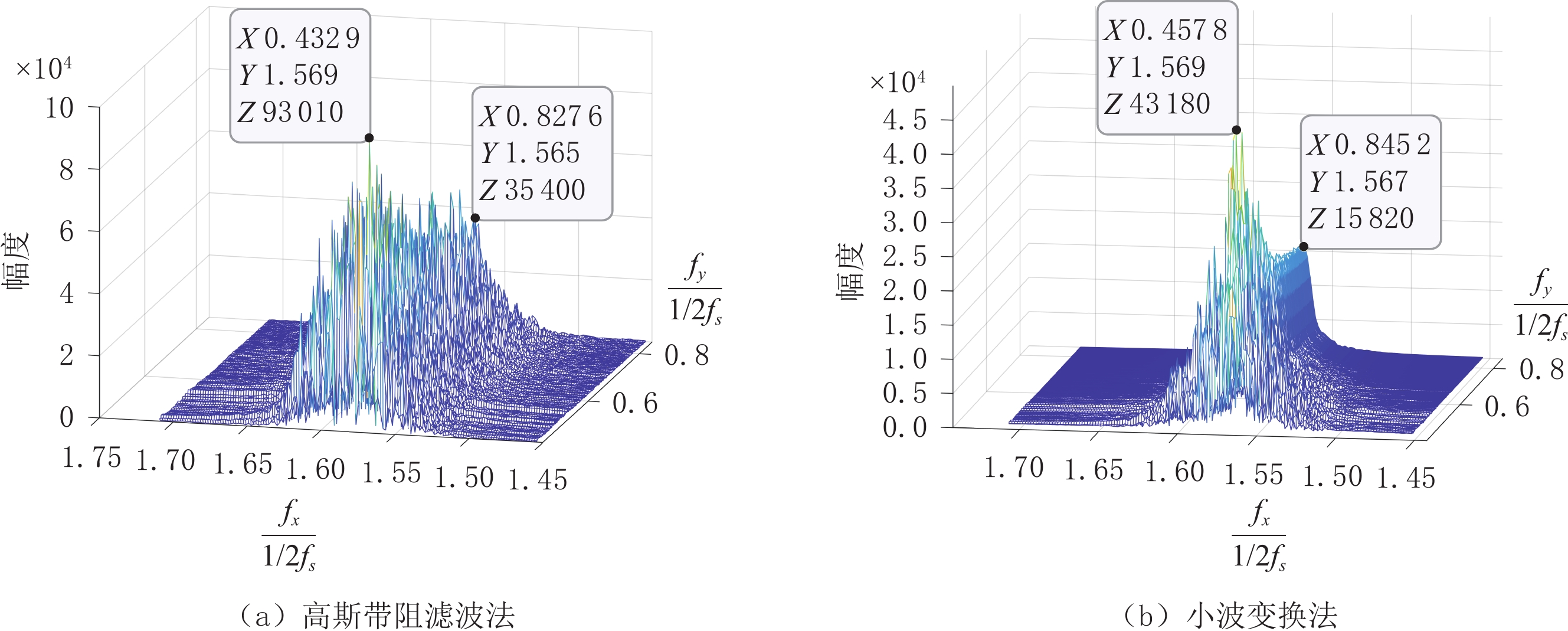
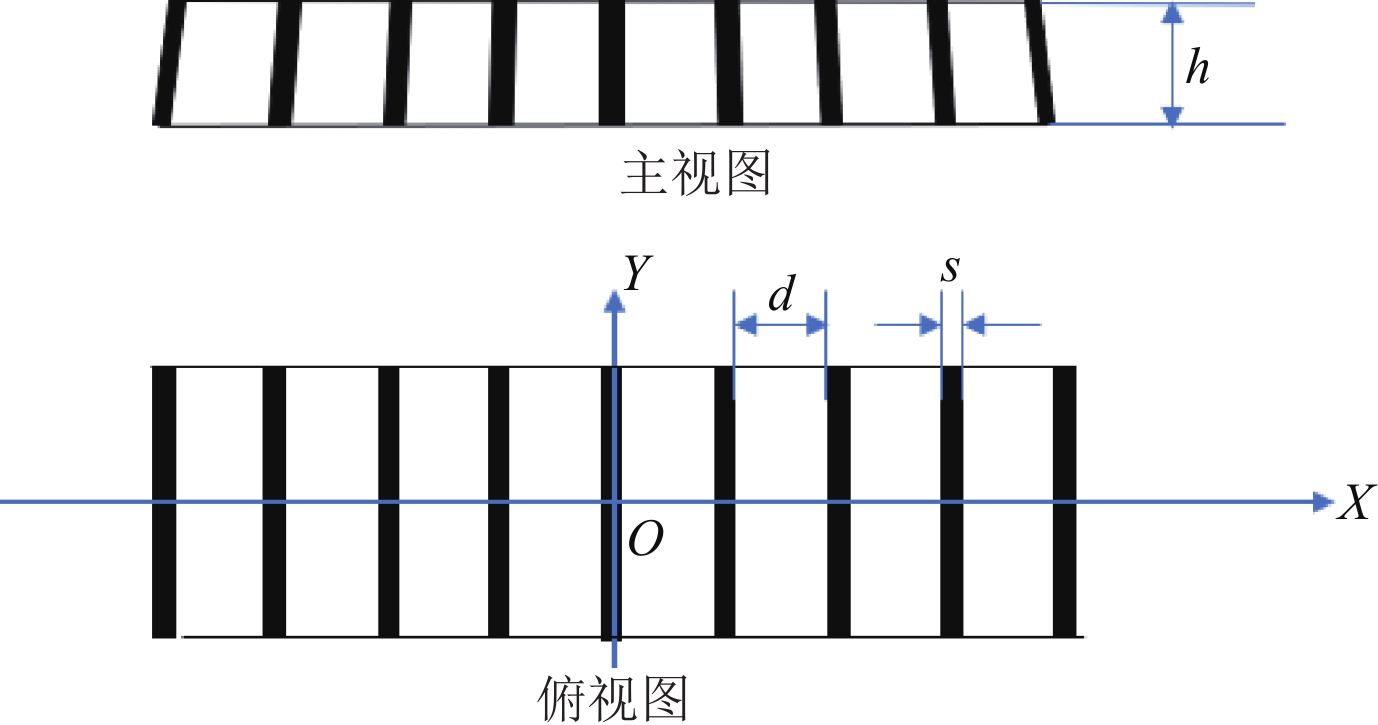
防散射滤线栅的结构如图1所示,滤线栅的黑色条带由吸收X射线的材料制成,其宽度s大约为几十微米,厚度h大约为几毫米。黑色条带之间的白色条带由能透过X射线的物质制成,间距d大约在几百微米。滤线栅是汇聚栅,越远离中心的黑色条带倾角越大,放置滤线栅时应保证X射线点源在滤线栅的焦线上。滤线栅的两个重要参数为光栅频率(grid frequency)和光栅比(grid ratio):光栅频率
$ {f}_{g}=\displaystyle\frac{1}{s+d} $ 决定了采样前滤线栅条纹的尖峰频率,光栅比$ \displaystyle\frac{h}{d} $ 决定了滤线栅阻止散射光子的能力。为叙述方便,以滤线栅的上表面中心为坐标原点$ O $ ,在滤线栅上表面建立二维直角坐标系$ O\text{-}XY $ ,其中$ X $ 轴垂直于黑色条带,$ Y $ 轴平行于黑色条带。防散射滤线栅通常紧贴平板探测器放置,其对平板探测器采集到的光强分布的影响取决于其对原X射线束及散射X射线束的透射率。滤线栅对原射线束的透射率依赖于射线打在的滤线栅上的位置,若打在白色条带上,其透射率接近于1,若打在黑色条带上,其透射率则远小于1。由于散射X射线束的方向杂乱无章,滤线栅对其透射率可用远小于1的常数来表征。因此在二维频域
$ {f}_{x}{f}_{y} $ 内的采样前滤线栅条纹各次谐波的尖峰频率$\Big({f}_{x,n},{f}_{y,n} \Big)$ 为:$$ \Big({f}_{x,n},\;{f}_{y,n}\Big)=\Big(n{f}_{g},\;0\Big),\;\;\;\;n=1, 2,\cdots 。 $$ (1) 平板探测器以空间频率
$ {f}_{s} $ 对采样前滤线栅条纹进行采样,由混叠效应,平板探测器探测到的滤线栅条纹的尖峰频率$\Big({f}_{sx,n},{f}_{sy,n}\Big)$ 为:$$ {f}_{sx,n}=\left|{f}_{x,n}-\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\left({f}_{x,n}/{f}_{s}\right)\times {f}_{s}\right| \text{,} $$ (2) $$ {f}_{sy,n}=\left|{f}_{y,n}-\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\left({f}_{y,n}/{f}_{s}\right)\times {f}_{s}\right| 。$$ (3) 式(2)与式(3)中的round表示取整到最近整数。特别地,滤线栅条纹基波尖峰频率
$\Big( {f}_{sx,1},{f}_{sy,1}\Big) $ 为:$$ {f}_{sx,1}=\left|{f}_{g}-\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\left(\frac{{f}_{g}}{{f}_{s}}\right)\times {f}_{s}\right| \text{,} $$ (4) $$ {f}_{sy,1}=0。 $$ (5) 2. 基于频谱拼接的小波变换条纹去除方法
2.1 总体思路
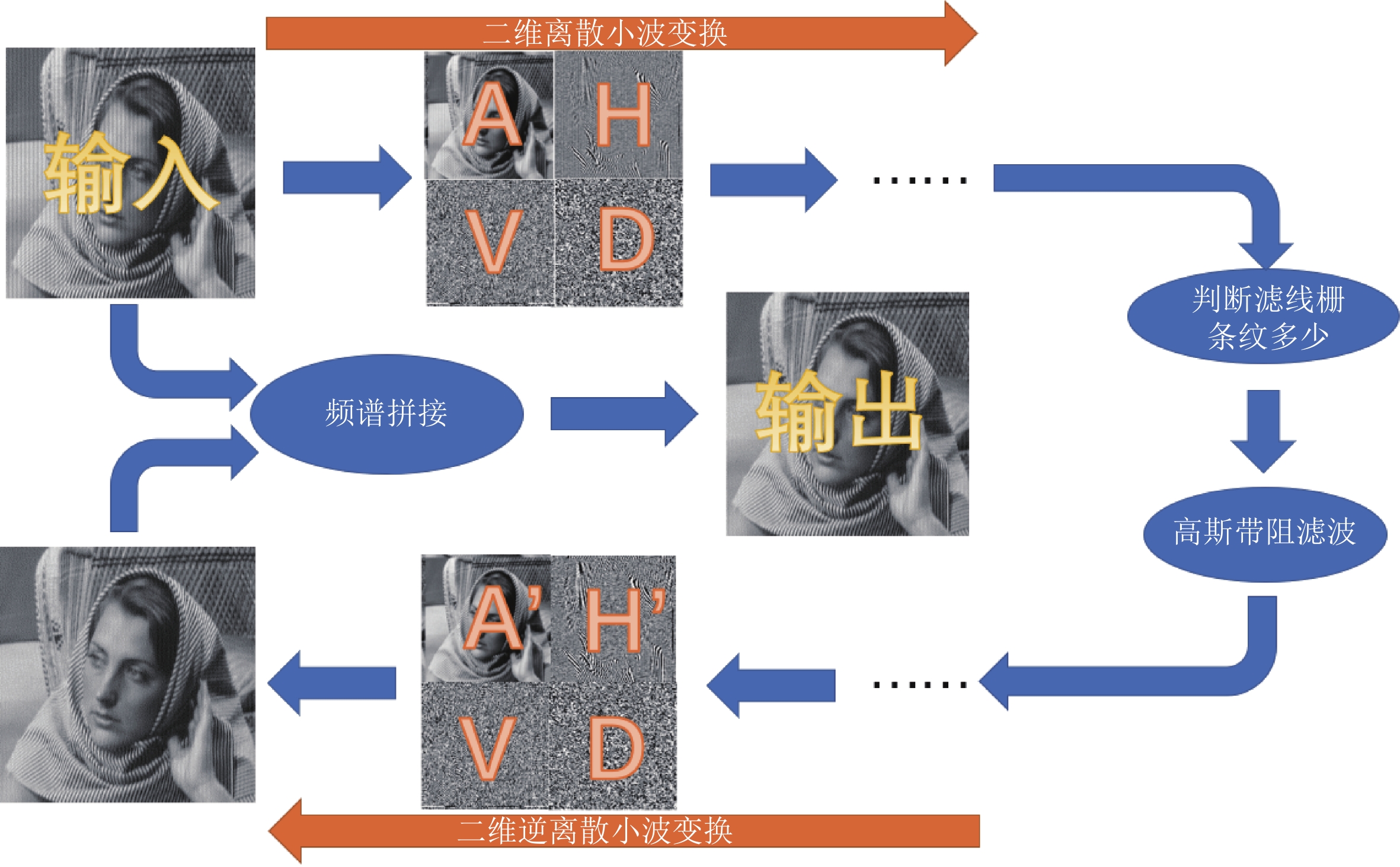
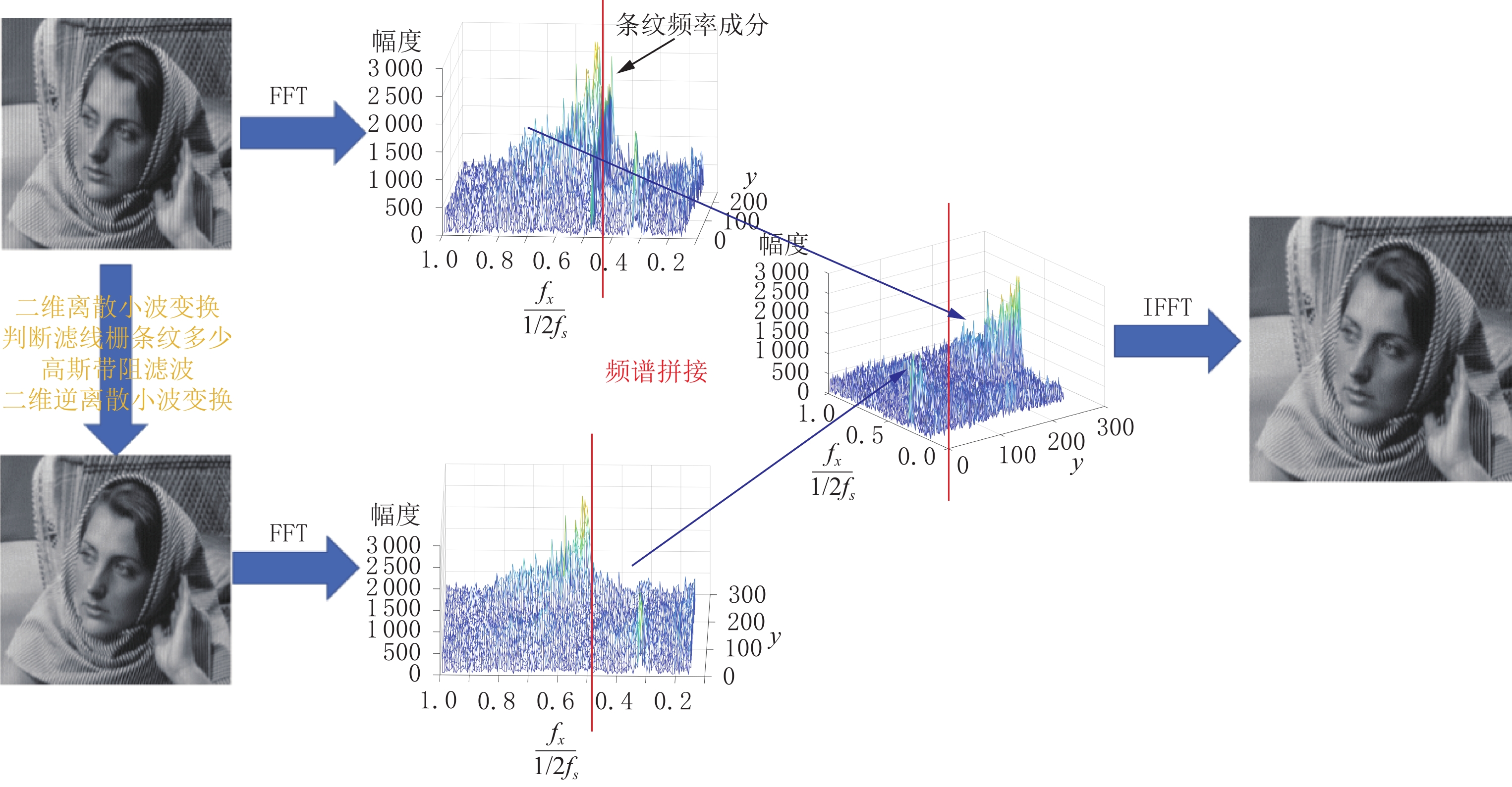
方法的整体思路如图2所示。对含有滤线栅条纹的图像做二维离散小波变换,原始图像被分解为分别含有其竖直方向高低频率成分、水平方向高低频率成分的4张子图A、H、V、D;对于沿竖直方向的滤线栅条纹,含有竖直方向高频频率成分的两张子图V和D一定不再含有滤线栅条纹,因而不再对V和D做进一步处理。对仍含有滤线栅条纹的子图继续做二维离散小波变换,直至其含有足够多的滤线栅条纹的空间特征;对具有足够多的滤线栅条纹的子图做高斯带阻滤波处理,以去除其中滤线栅条纹,并做二维逆离散小波变换以将图像还原;还原得到的图像虽不再含有滤线栅条纹,但其含有小波变换谐波,因而将其与原始图像做频谱拼接并得到最终的输出。
2.2 递归的二维离散小波变换
从信号处理的角度,一维离散小波变换是将离散时间信号分别通过高通滤波器和低通滤波器并向下采样,从而将该信号分解为高频成分和低频成分。二维离散小波变换建立在一维离散小波变换的基础之上:对一张大小为M×N的光强分布图
$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ ,先对M行逐行做一维离散小波变换,从而将其分解为两张大小为M×$\displaystyle\frac{N}{2}$ 的子图,再对每张子图的$\displaystyle\frac{N}{2}$ 列逐列做一维离散小波变换,从而将原图$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ 分解为4张大小为$\displaystyle\frac{M}{2}$ ×$\displaystyle\frac{N}{2}$ 的子图,分别记作A、H、V、D。其中,A为图像$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ 中竖直方向低频、水平方向低频成分;H为图像$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ 中水平方向高频、竖直方向低频成分;V为图像$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ 中水平方向低频、竖直方向高频成分;D为图像$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}}\mathrm{中} $ 竖直方向高频、水平方向高频成分。不妨认为滤线栅条纹沿竖直方向(若滤线栅条纹不沿竖直方向,则可旋转图像至滤线栅条纹竖直),则滤线栅条纹的基波频率成分必然属于竖直方向低频成分,所以子图D和V中不可能含有滤线栅条纹基波频率成分。而子图A和H中是否含有滤线栅条纹的基波频率成分,取决于滤线栅条纹基波尖峰频率
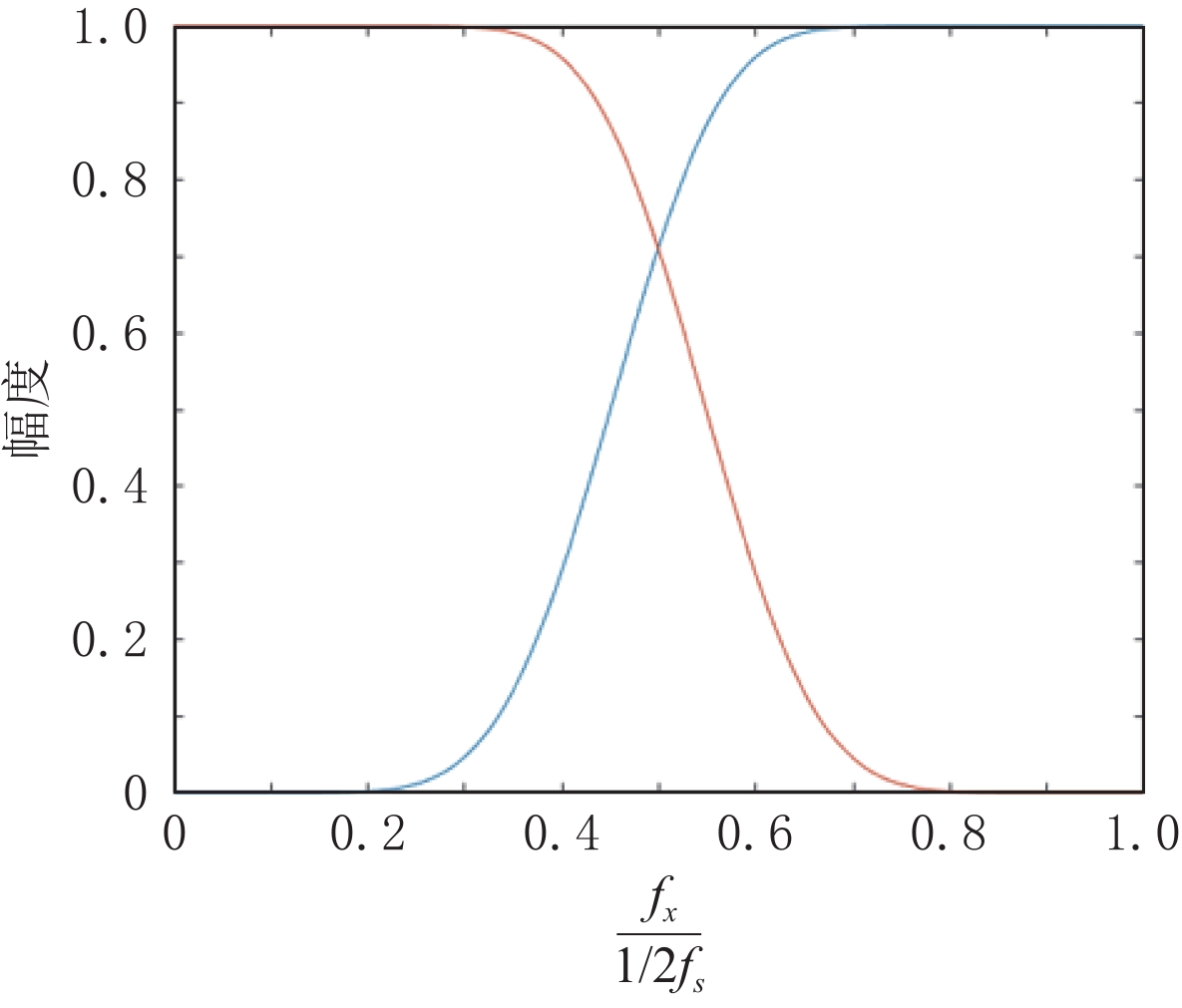
$ {f}_{sx,1} $ 与奈奎斯特频率$\displaystyle\frac{1}{2}{f}_{s}$ 的比值和所使用的小波基。小波基的选择应考虑两点:①高通滤波器与低通滤波器应接近于理想滤波器,即通频带的重叠应尽可能的少,从而将信号的高频频谱与低频频谱尽可能的完美分开;②滤波器的长度越长,滤波所需的时间代价越高。若给定滤波器的长度,多贝西小波在时域中表现得最为光滑,因而在频域中最为接近于理想滤波器。本文选择的小波基为第10层多贝西小波。
第10层多贝西小波的低通和高通滤波器的响应函数的幅度谱如图3所示。只有不到5% 的频率大于0.7倍的奈奎斯特频率的频率成分可以通过低通滤波器。因此,当
$\displaystyle\frac{{f}_{sx,1}}{{1}/{2}{f}_{s}}\le 0.7$ 时,认为A中含有滤线栅条纹的基波频率成分,否则,认为A中不含有滤线栅条纹的基波频率成分。类似的可判断子图H中是否含有滤线栅条纹的基波频率成分。本文提出的滤线栅条纹去除方法,针对于去除滤线栅条纹的基波。因此,对不含有滤线栅条纹基波的子图无需做任何处理;而对含有滤线栅条纹基波的子图,需进一步对其递归地做二维离散小波变换,直到子图中滤线栅条纹的特征已足够明显。
2.3 滤线栅条纹明显程度的表征
在空间域中,滤线栅条纹的明显程度可用灰度共生矩阵的统计量来表征。灰度共生矩阵(grey level co-occurrence matrix)由灰度图G和空间约束r(spatial relationship)来定义。空间约束r用距离d和角度
$ \phi $ 定义,记作$(d,\; \phi) $ ,称灰度图G上的两个点$ {\boldsymbol{x}}_{1}、 $ $ {\boldsymbol{x}}_{2} $ 满足空间约束r当且仅当$ {\boldsymbol{x}}_{1} $ 与$ {\boldsymbol{x}}_{2} $ 的欧氏距离为d个像素,且$ {\boldsymbol{x}}_{1} $ 到$ {\boldsymbol{x}}_{2} $ 的连线与灰度图G的水平方向夹角为$ \phi $ 。定义集合$ {P}_{r,ij} $ :$$ {P}_{r,ij}=\left\{({\boldsymbol{x}}_{1},{\boldsymbol{x}}_{2})\left|\begin{array}{c}灰度图\;{\boldsymbol{G}}\;在\;{\boldsymbol{x}}_{1}处灰度为i\text{,}在\;{\boldsymbol{x}}_{2}处\\灰度为j\text{,} 且\;{\boldsymbol{x}}_{1}、{\boldsymbol{x}}_{2}\;满足空间约束\;{\boldsymbol{r}}\end{array}\right.\right\} 。 $$ (6) 若灰度图G的灰度级的数量为
$A $ ,则由灰度图G和空间约束r定义的灰度共生矩阵$ {\boldsymbol{P}}_{\boldsymbol{r}}\left(\boldsymbol{G}\right) $ 是一个$ A\times A $ 的方阵,且每个元素$ {p}_{ij} $ 为集合$ {P}_{r,ij} $ 的基数:$$ {\boldsymbol{P}}_{\boldsymbol{r}}\left(\boldsymbol{G}\right)={\left\{{p}_{ij}\right\}}_{A\times A} \text{,} $$ (7) $$ {p}_{ij}=\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}\left({P}_{r,ij}\right) 。 $$ (8) 式(8)中
$ \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d} $ 表示取集合的基数。常用于衡量灰度图中滤线栅条纹明显程度的统计量为相关度(Correlation)和对比度(Contrast)。相关度定义为:$$ {\rm{Correlation}}=\sum _{i=0}^{A-1}\sum _{j=0}^{A-1}\frac{{p}_{ij}\left(i-{\mu }_{i}\right)\left(j-{\mu }_{j}\right)}{{\sigma }_{i}{\sigma }_{j}} \text{,} $$ (9) 其中:
$$ {\mu }_{i}=\sum _{i=0}^{A-1}\sum _{j=0}^{A-1}\left({p}_{ij}\times i\right) \text{,} $$ (10) $$ {\mu }_{j}=\sum _{i=0}^{A-1}\sum _{j=0}^{A-1}\left({p}_{ij}\times j\right) \text{,} $$ (11) $$ {\sigma }_{i}=\sqrt{\sum _{i=0}^{A-1}\sum _{j=0}^{A-1}\left({p}_{ij}\times {\left(i-{\mu }_{i}\right)}^{2}\right)} \text{,} $$ (12) $$ {\sigma }_{j}=\sqrt{\sum _{i=0}^{A-1}\sum _{j=0}^{A-1}\left({p}_{ij}\times {\left(j-{\mu }_{j}\right)}^{2}\right)} 。 $$ (13) 对比度Contrast定义为:
$$ {\rm{Contrast}}=\sum _{i=0}^{A-1}\sum _{j=0}^{A-1}{p}_{ij}{\Big|i-j\Big|}^{2} 。 $$ (14) 用下式可判断灰度图
${\boldsymbol{G}} $ 中是否含有足够多的沿竖直方向的滤线栅条纹:$$ {\rm{Correlation}}\Big({\boldsymbol{P}}_{(2, 90^\circ)}\left(\boldsymbol{G}\right)\Big)-{\rm{Correlation}}\Big({\boldsymbol{P}}_{(2, 0^\circ)}\left(\boldsymbol{G}\right)\Big) > {\varepsilon }_{1} \text{,} $$ (15) $$ {\rm{Contrast}}\Big({\boldsymbol{P}}_{(2,0^\circ)}\left(\boldsymbol{G}\right)\Big) > {\varepsilon }_{2} 。 $$ (16) 式(15)与式(16)中的
$ {\varepsilon }_{1} $ 、$ {\varepsilon }_{2} $ 为可调参数。式(15)与式(16)同时满足,表明灰度图${\boldsymbol{G}} $ 中已含有足够多的竖直方向的滤线栅条纹。之所以要判断二维离散小波变换得到的各个子图中是否含有足够多的滤线栅条纹,是因为小波变换的本质是对滤线栅条纹在其频域进行“聚焦”。若“聚焦”得不充分,直接用高斯带阻滤波除滤线栅条纹,则会造成较多的物体细节信息的损失。2.4 高斯带阻滤波
对于沿竖直方向的滤线栅条纹,可用一维的高斯带阻滤波器对图像逐行处理。高斯带阻滤波器对长度为M的离散时间信号的频率响应函数
$ B\left(u\right) $ 为:$$ B\left(u\right)=\left(1-\exp\left({-\frac{1}{2}{\left(\frac{u-\mu }{\sigma }\right)}^{2}}\right)^{^{}}\right)\left(1-{\exp}\left({-\frac{1}{2}{\left(\frac{u-(M-\mu )}{\sigma }\right)}^{2}}\right)^{^{}}\right) 。 $$ (17) 式(17)中
$u=\mathrm{0,1},2,\cdots, M-1$ 。$ \mu $ 为滤线栅条纹基波在一维离散傅里叶变换频谱中的实际峰位,$ \sigma $ 表征了滤线栅条纹基波在一维离散傅里叶变换频谱的峰宽。滤线栅条纹基波在一维离散傅里叶变换频谱的理论计算峰位$ {\mu }' $ 为:$$ {\mu }'=M\times {f}_{sx,1}\div{f}_{s} 。 $$ (18) 若用理论计算峰位
$ {\mu }' $ 直接作为实际峰位$ \mu $ 的估计,通常会产生较大的偏差。对此,取以$ {\mu }' $ 为中心,宽度为W的区间$U=\left[{\mu }'-\displaystyle\frac{1}{2}W,\;{\mu }'+\frac{1}{2}W\right]$ ,将$ u $ 视为随机变量,并将待滤波序列的离散傅里叶变换幅度谱视为随机变量$ u $ 的概率质量函数,计算$ u $ 在区间$ U $ 内的平均值${\mu }''$ ,并以${\mu }''$ 作为实际峰位$ \mu $ 的最终估计。同时,计算随机变量$ u $ 在区间$ U $ 内的标准差${\sigma }''$ ,以${\sigma }''$ 作为$ \sigma $ 的最终估计值。区间
$ U $ 的宽度W的选取至关重要,W选得过大,则会损失较多的物体信息,而W选得过小,又会引起对实际峰位$ \mu $ 估计偏差较大,滤线栅条纹除不干净等问题。因为小波变换本身不会改变一维离散傅里叶变换频谱中滤线栅条纹基波的峰宽,所以可将宽度W作为小波变换法除滤线栅条纹的超参数,并加以调节。2.5 频谱拼接
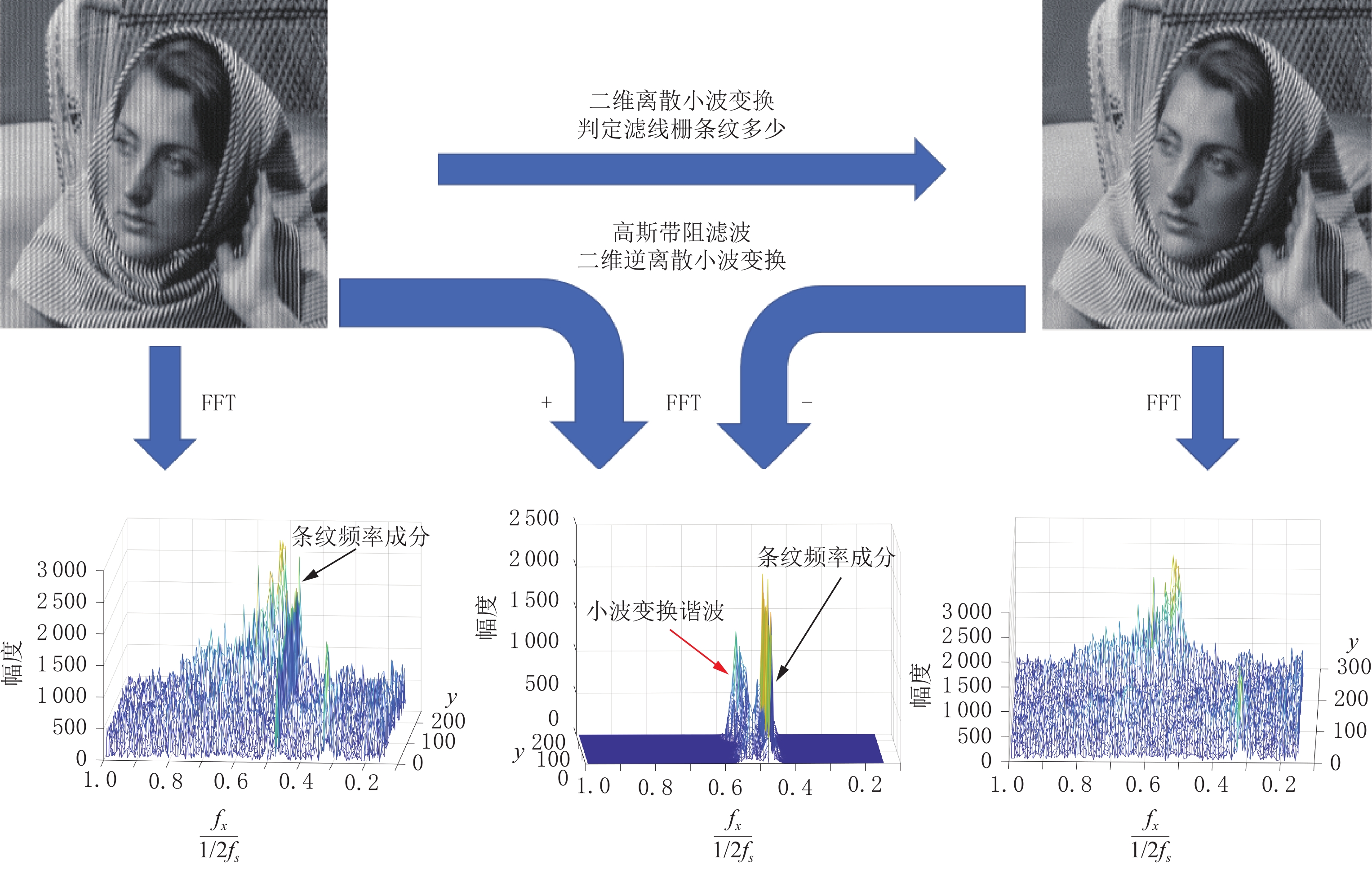
频谱拼接的必要性如图4所示。经二维逆离散小波变换还原后的图像频谱与原图像频谱除在条纹频率成分附近有明显差异外,在与条纹频率关于0.5倍的奈奎斯特采样频率对称的频率成分处也有明显差异,这就是小波变换谐波。小波变换谐波的产生是由于小波变换中高通与低通滤波器的通频带有重叠,从而高频频谱与低频频谱没有完美的分开,因而用高斯带阻滤波滤除高频(或低频)频谱中的滤线栅条纹时,同时影响了原频谱中低频(或高频)频率成分。
产生小波变换谐波的根本原因是:处理高频(或低频)频谱对低频(或高频)成分具有破坏性。因此,用频谱拼接的方式可以弥补去除滤线栅条纹时对频谱造成的破坏(图5)。如果条纹频率成分在原图像频谱的低频部分,则对二维逆小波变换还原图像的每一行,抛弃其高频成分,并用原图像对应行的高频成分加以代替,作为最终输出。经频谱拼接后输出的图像既不含有滤线栅条纹,也不会含有小波变换谐波。
为进一步展示频谱拼接的效果,本文做了模拟实验,对原图人为施加条纹[10],并用小波变换方法加以去除。做与不做频谱拼接得到的图像视觉效果及其与原图的差异如图6所示,经频谱拼接得到的图像明显与原图更为接近。频谱拼接的定量效果如表1所示,频谱拼接可以明显改善输出图像的峰值信噪比(peak signal-to-noise ratio)、与原图的结构相似性(structural Similarity)[11]、与原图差异的标准差等统计参数,因而引入频谱拼接可以更好的保留原图像中的细节信息。
表 1 频谱拼接的定量效果Table 1. Quantitative effect of spectrum coalescence统计参数 加条纹图像 不做频谱拼接图像 做频谱拼接图像 峰值信噪比 29.719 34.475 37.758 结构相似性 0.984 0.995 0.998 与原图差异的标准差 9.122 5.085 3.458 2.6 方法总结
总得来说,基于频谱拼接的小波变换条纹去除方法可分为6步:
(1)由采样频率
$ {f}_{s} $ 和光栅频率$ {f}_{g} $ 计算滤线栅条纹基波的尖峰频率$ {f}_{sx,1} $ 。(2)对二维图像
$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ 做二维离散小波变换DWT,得到4张子图A、H、V、D。(3)判断子图A中是否含有滤线栅条纹的基波频率成分。若没有,则把子图A标记为
$ {\boldsymbol{A}}{\boldsymbol{'}} $ ,并跳过第4步。(4)利用灰度共生矩阵的统计量判定A中竖直方向的滤线栅条纹是否足够明显。若判定为是,则对A逐行做高斯带阻滤波,以除去滤线栅条纹,得到不含滤线栅条纹的子图
$ {\boldsymbol{A}}{\boldsymbol{'}} $ ;若判定为否,则将A视为采样频率减半的光强分布图$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ ,递归的用正在描述的基于频谱拼接的小波变换条纹去除方法来去除A中的滤线栅条纹,获得$ {\boldsymbol{A}}{\boldsymbol{'}} $ 。(5)对子图H做类似操作,以获得不含滤线栅条纹的子图
$ {\boldsymbol{H}}{\boldsymbol{'}} $ 。(6)用
$ {\boldsymbol{A}}{\boldsymbol{'}} $ 替换A,用$ {\boldsymbol{H}}{\boldsymbol{'}} $ 替换H,并对$ {\boldsymbol{A}}{\boldsymbol{'}} $ 、$ {\boldsymbol{H}}{\boldsymbol{'}} $ 、$ \boldsymbol{V} $ 、$ \boldsymbol{D} $ 做二维离散反小波变换,得到还原图像$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n},0} $ ,并对$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n}} $ 与$ {\boldsymbol{I}}_{\boldsymbol{m}\boldsymbol{n},0} $ 做频谱拼接,得到既无滤线栅条纹,也不含小波变换谐波的光强分布图像${\boldsymbol{I}}'_{\boldsymbol{m}\boldsymbol{n}}$ ,作为最终输出。3. 基于频谱拼接的小波变换条纹去除方法的实验检验
3.1 实验描述
锥束CT实验装置如图7所示,主要包括X射线源、转台、防散射滤线栅、平板探测器4个组成要素。由于平板探测器较小,被防散射滤线栅遮挡,在图7中并不可见。实验所使用的X射线源为日本滨松公司生产的微焦点X射线源L12161-07,微焦点尺寸为50 μm;使用的防散射滤线栅是JPI Healthcare Solutions公司生产的防散射滤线栅JPI GRID-1000,其由高吸收的栅条Pb和低吸收的缝隙Al并列排列而成,光栅比为10,焦距为100 cm,光栅周期为127 μm;使用的平板探测器为滨松公司生产的平板探测器1412 f,其每行有1212个像素,每列有1400个像素,采样周期为100 μm。采样时,X射线管电压设为80 kV,X射线管电流设为500 μA,平板探测器的帧率设为12 fps,X射线源到平板探测器的距离为997 mm,转台到平板探测器的距离为340 mm,滤线栅与平板探测器紧贴。
实验总共采集3组数据:第1组实验数据是X射线源与平板探测器间只有滤线栅而没有模体时,平板探测器测到的光强分布,共采集了20帧,两帧之间转台旋转18°,这组数据将被称为“空气”;第2组实验数据是将矿泉水放在转台上作为模体,滤线栅紧贴平板探测器放置时,平板探测器测到的光强分布,共采集了216帧,每两帧之间转台旋转1.67°,这组实验数据将被称为“水”;第3组实验数据是将装有老鼠的试管放在转台上作为模体,滤线栅紧贴平板探测器放置时,平板探测器测到的光强分布,共采集216帧,每两帧之间转台旋转1.67°,这组实验数据将被称为“老鼠”。此外,还采集了平板探测器的本底数据。
3.2 检验小波变换方法有效性的实验设计
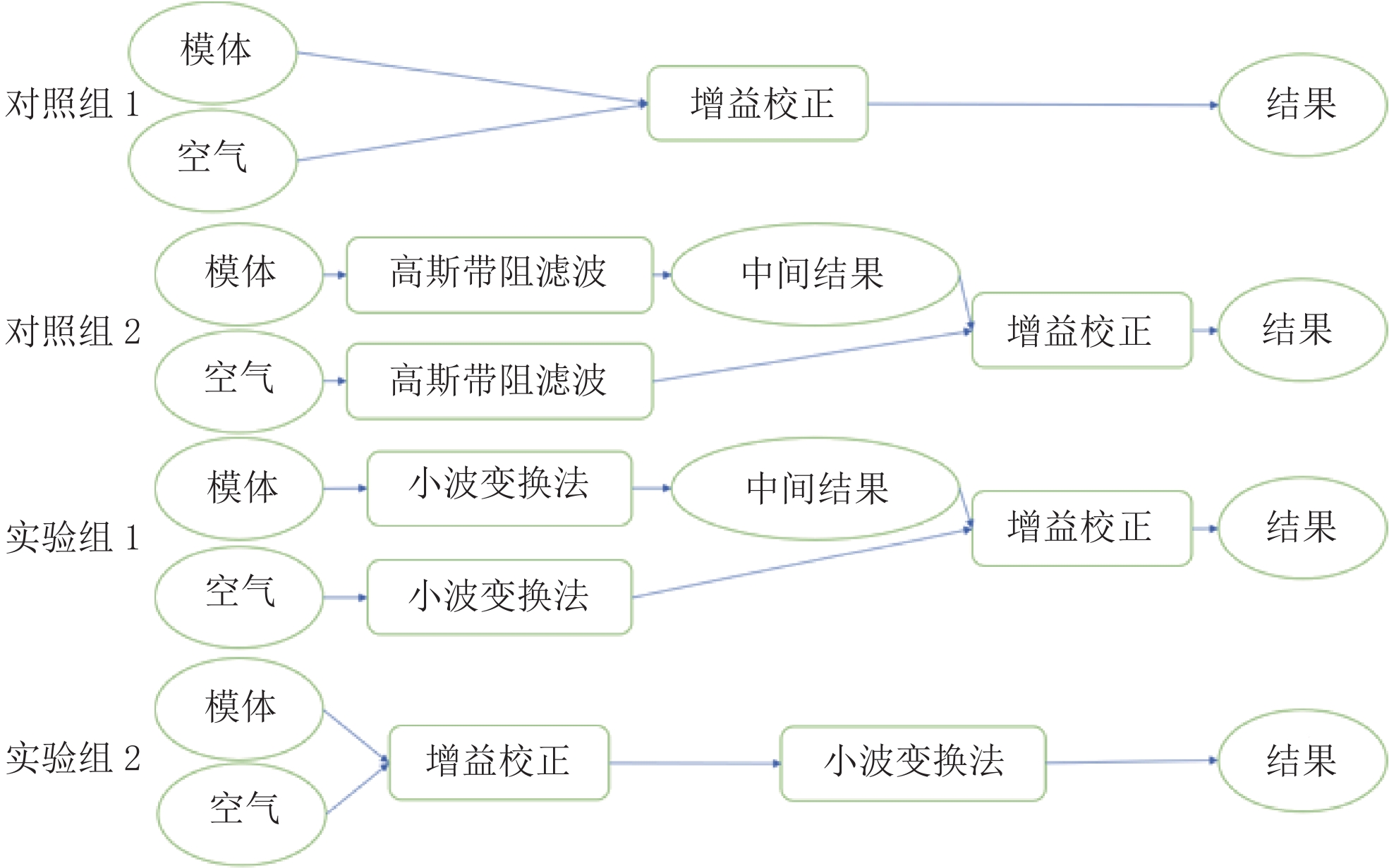
为检验本文提出的基于频谱拼接的小波变换方法(简称为小波变换法)去除滤线栅条纹的效果而设计的对照实验如图8所示。对照组1用“空气”直接对模体做增益校正,既校正平板探测器每个像素对X射线的灵敏度差异,又校正滤线栅条纹;对照组2与实验组1先分别用高斯带阻滤波法[8]或是小波变换法对“空气”和模体原始数据加以处理,再做增益校正以校正平板探测器的每个像素对X射线的灵敏度差异;实验组2先做增益校正,既校正平板探测器的灵敏度差异,又除去一定的滤线栅条纹,再用小波变换法将剩余滤线栅条纹除去。
实验组1的中间结果与模体的原始数据对比,可以体现出小波变换法对滤线栅条纹的去除效果;实验组1的中间结果与对照组2的中间结果对比,体现出小波变换法损失物体信息的多少;实验组1、实验组2的结果与对照组1的结果对比,体现出将小波变换法应用于增益校正前或是增益校正后对滤线栅条纹及CT重建图像中环状伪影的影响。
3.3 小波变换方法的条纹去除效果
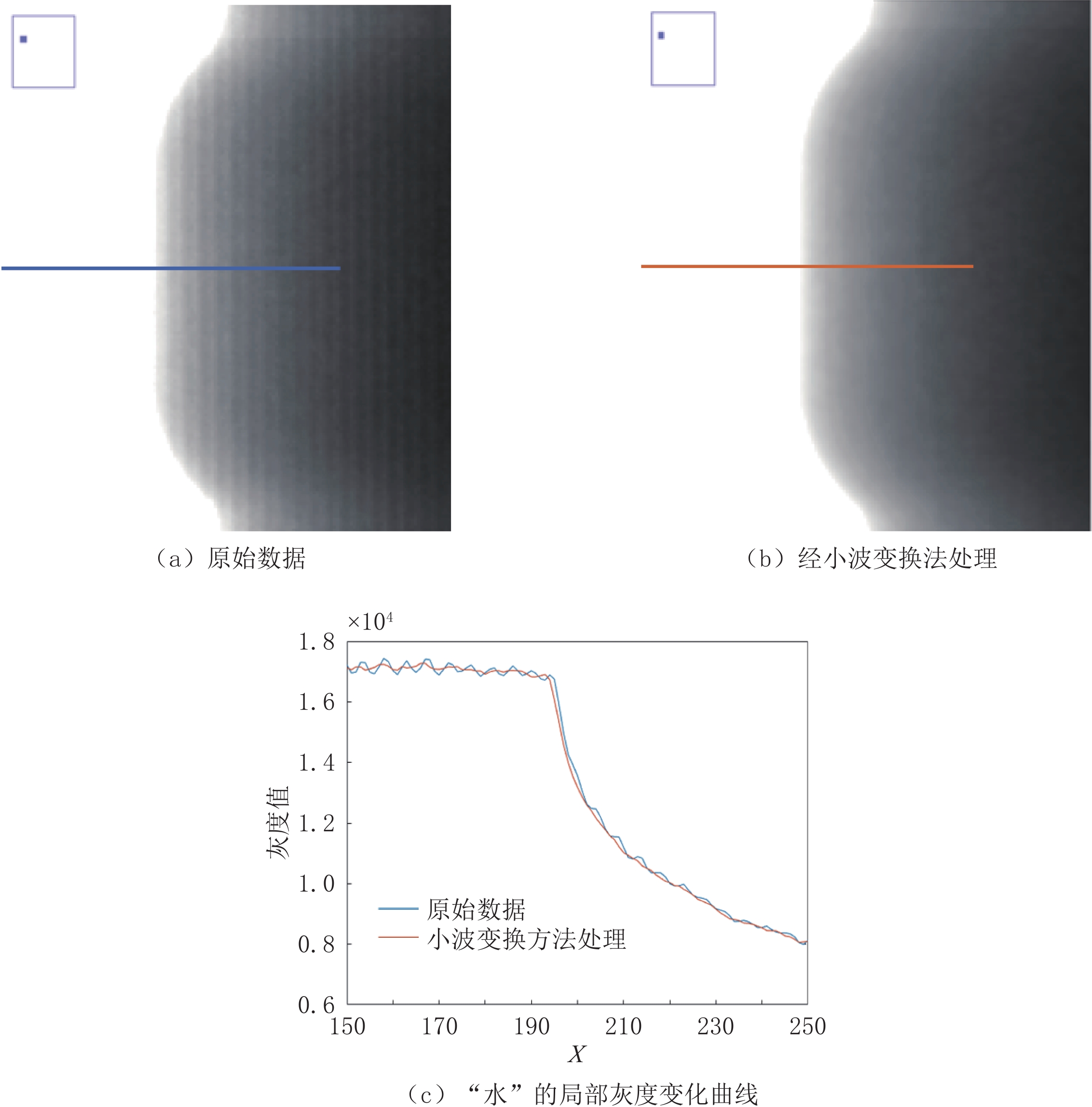
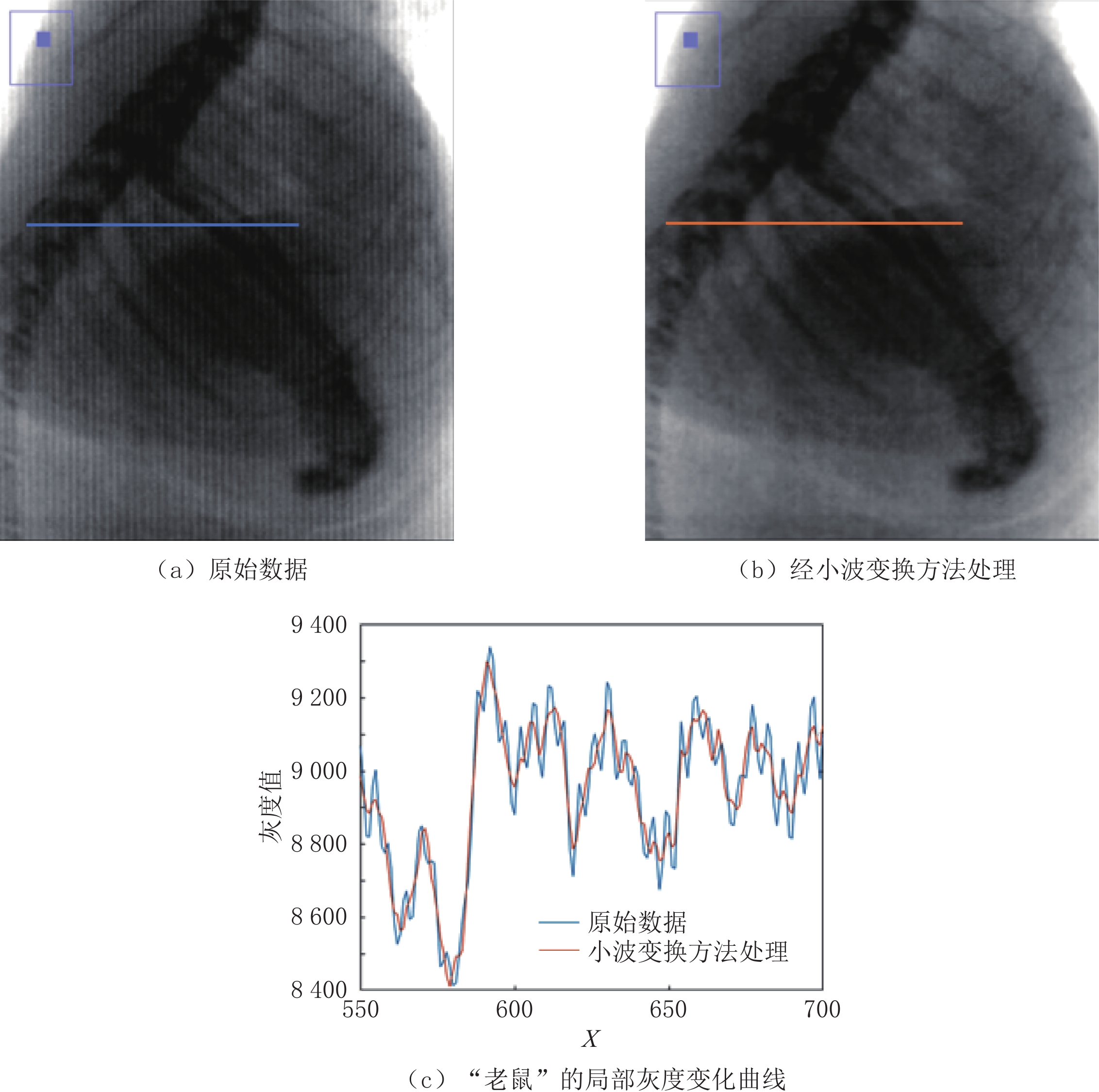
“水”和“老鼠”在小波变换法处理前后的图像如图9(a)和图9(b)、图10(a)和图10(b)所示。小波变换法处理后,已观察不到明显的滤线栅条纹,而且小波变换法还很好地保留了小鼠体内的细节信息。“水”和“老鼠”在小波变换法处理前后的局部灰度变化曲线如图9(c)和图10(c)所示,小波变换处理后的灰度曲线很好地保留了原灰度曲线的总体变化趋势,并很好地抑制了原灰度曲线中由于滤线栅条纹引起的灰度值波动。
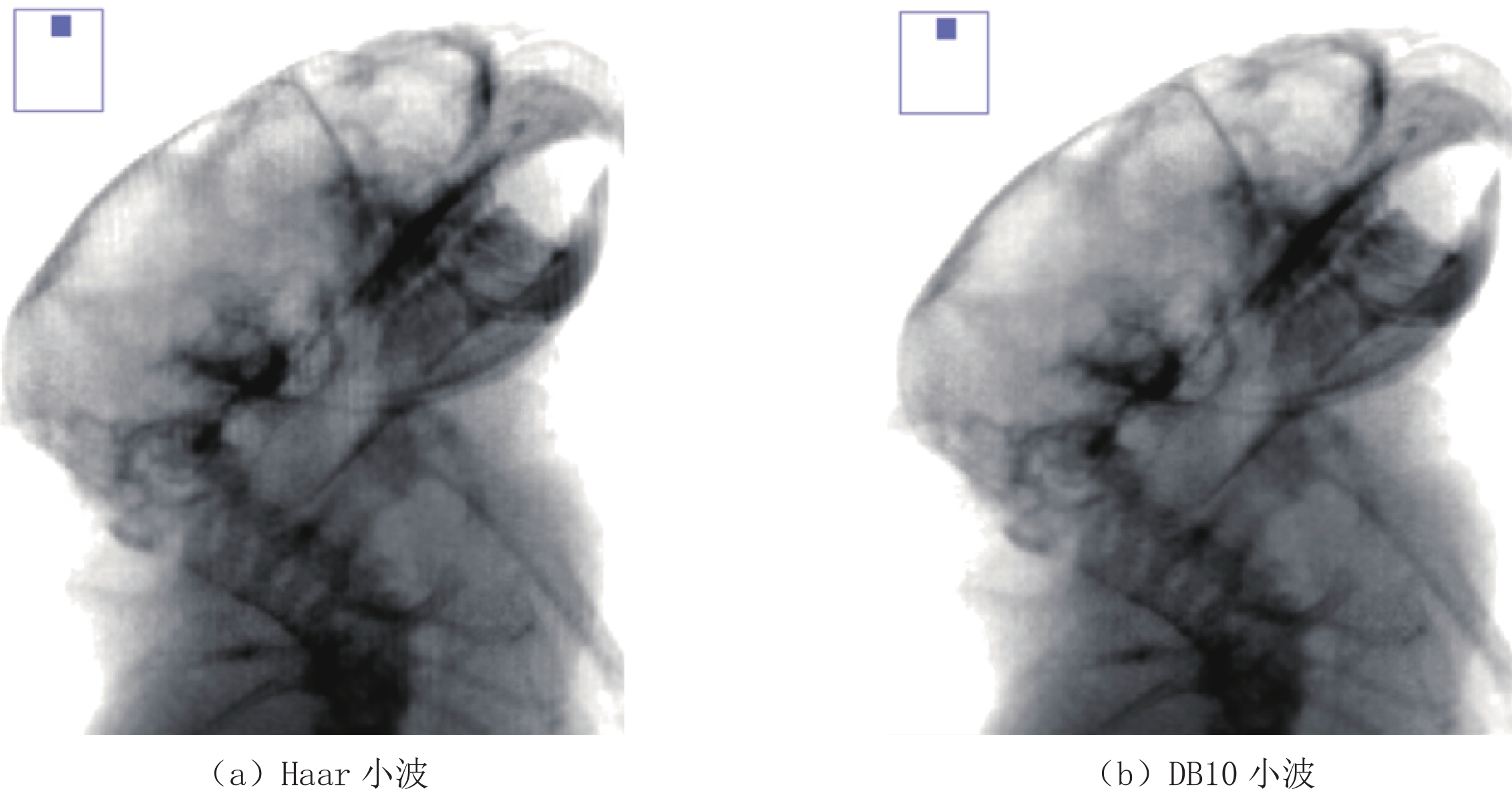
为体现本文小波基选择的合理性,分别用Haar小波和本文采用的DB10小波对“老鼠”加以处理,效果如图11所示。相比于DB10小波处理后的“老鼠”,Haar小波处理后的“老鼠”中仍能观察到较为明显的沿竖直方向的滤线栅条纹,这说明不能选用过于短的小波基。
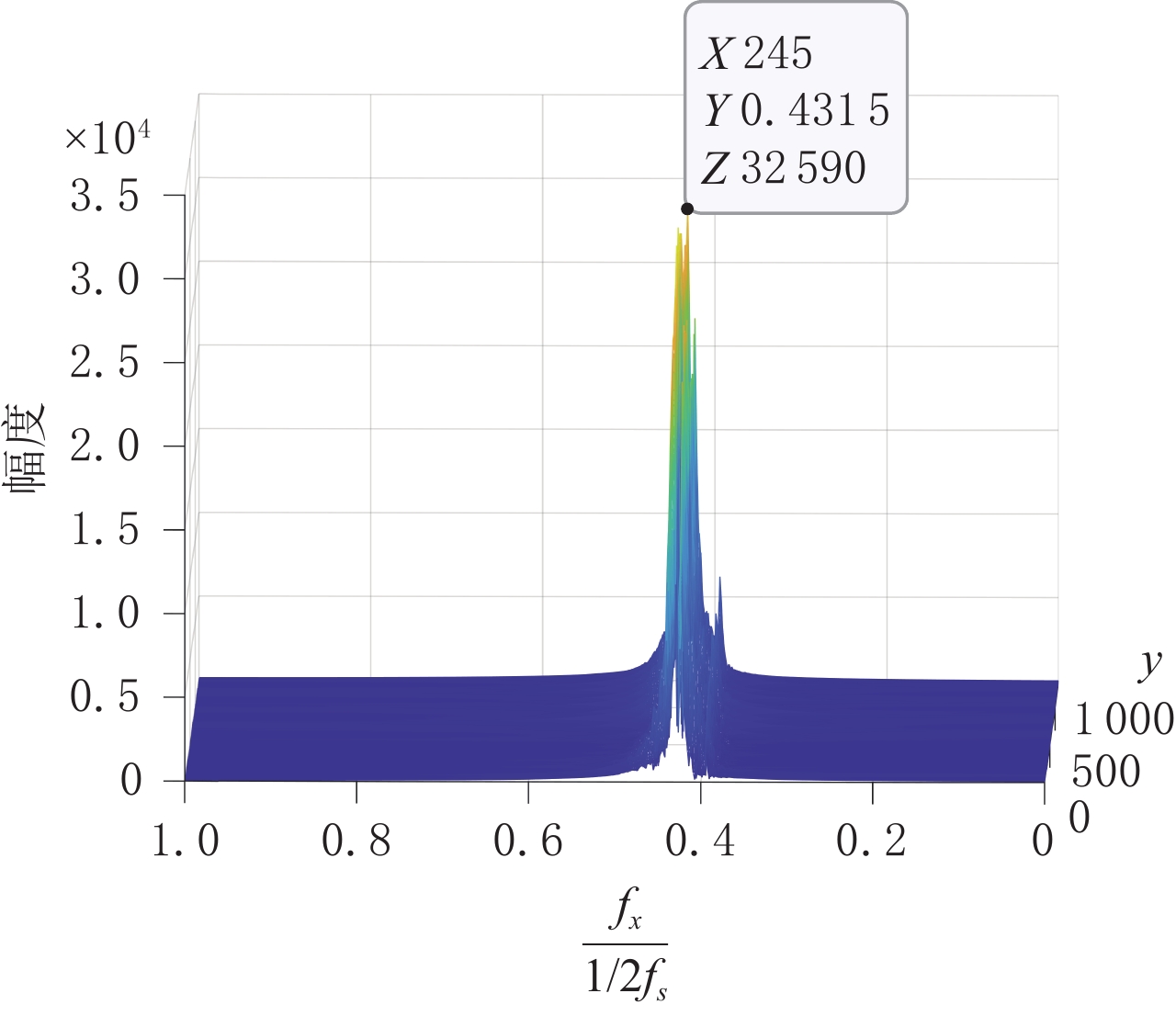
“水”在小波变换法处理前后的差异的一维离散傅里叶变换幅度谱如图12所示。由式(4),理论计算得到的滤线栅条纹基波尖峰频率为
$\displaystyle\frac{{f}_{sx,1}}{{1}/{2}{f}_{s}}=0.425$ ,这表明基于频谱拼接的小波变换方法处理前后的频谱仅仅在滤线栅条纹基波的尖峰频率附近有明显差异,而不会引入小波变换谐波。由于实验得到的滤线栅条纹沿竖直方向,在二维频域
$ {f}_{x}{f}_{y} $ 平面内,滤线栅条纹的尖峰频率在fx轴附近,远离fx轴的频率成分反映了原物体信息,因此在去除滤线栅条纹时不希望对远离fx轴的频率成分造成影响。图13给出了“水”在高斯带阻滤波或小波变换法处理前后的差异的二维离散傅里叶变换幅度谱中远离fx轴的局部。相比高斯带阻滤波法,小波变换法处理前后远离fx轴的频率成分的改变更少,因而损失的物体信息更少。图14给出了“水”经对照组1、实验组1、实验组2分别处理后的一维离散傅里叶变换幅度谱。无论将小波变换法应用于增益校正前或增益校正后以去除滤线栅条纹,均可将直接增益校正后残留的滤线栅条纹的基波频率成分除去。
图15和图16分别给出了“水”和“老鼠”经对照组1、实验组1、实验组2分别处理后,通过FDK重建算法得到的CT重建图像的局部。在增益校正前或增益校正后应用小波变换法,可以除去直接增益校正得到的CT重建图像中残留的环状伪影。从实验组1和实验组2的CT重建图像中不能观察到明显区别,因此小波变换法去除滤线栅条纹既可应用于增益校正前,也可应用于增益校正后。
4. 总结
防散射滤线栅在阻止散射光子到达平板探测器的同时会引入滤线栅条纹。滤线栅条纹具有空间域特征和频域特征:在空间域上,灰度共生矩阵的统计量可以反应滤线栅条纹的明显程度;在频域上,滤线栅条纹集中分布在滤线栅条纹尖峰频率附近。综合利用滤线栅条纹空间域特征和频域特征的小波域抑制方法相比于空间域方法和频域滤波方法具有明显优势。
本文创新性地提出了基于频谱拼接的小波变换条纹去除方法,既能在损失物体细节信息少的前提下很好地去除滤线栅条纹,又不会引入小波变换谐波;并通过实验检验了该方法的有效性。期待本项研究能进一步提升锥束CT重建图像的均一度,并推动锥束CT在医疗、工业无损检测等领域的进一步发展。
-
表 1 频谱拼接的定量效果
Table 1 Quantitative effect of spectrum coalescence
统计参数 加条纹图像 不做频谱拼接图像 做频谱拼接图像 峰值信噪比 29.719 34.475 37.758 结构相似性 0.984 0.995 0.998 与原图差异的标准差 9.122 5.085 3.458 -
[1] 庄天戈. CT原理与算法[M]. 1版. 上海: 上海交通大学出版社, 1992. [2] 金慧君, 张蔚, 焦启刚, 等. 应用于口腔医学的锥束CT技术[J]. 口腔材料器械, 2011,20(3): 158−161. JIN H J, ZHANG W, JIAO Q G, et al. Technique of cone-beam computed tomography for oral clinical practice[J]. Oral Material and Equipment, 2011, 20(3): 158−161. (in Chinese).
[3] 吴彦举, 郝冰, 常华峰, 等. 工业锥束CT在直升机承力件检测方面的应用[J]. 新型工业化, 2020,10(5): 67−69. [4] FELDKAMP L A, DAVIS L C, KRESS J W. Practical cone-beam algorithm[J]. Journal of the Optical Society of America A, 1984, 1(6): 612−619. doi: 10.1364/JOSAA.1.000612
[5] RÜHRNSCHOPFA E P, KLINGENBECK K. A general framework and review of scatter correction methods in X-ray cone-beam computerized tomography. Part 1: Scatter compensation approaches[J]. Medical Physics, 2011, 38(7): 4296−4311. doi: 10.1118/1.3599033
[6] RÜHRNSCHOPFA E P, KLINGENBECK K. A general framework and review of scatter correction methods in X-ray cone-beam computerized tomography. Part 2: Scatter estimation approaches[J]. Medical Physics, 2011, 38(9): 5186−5199. doi: 10.1118/1.3589140
[7] KIM D S, LEE S, YOON J K. Grid artifact reduction based on homomorphic filtering in digital radiography imaging[J]. Proc. of SPIE, 2013, 8668: 86682C-1−86682C-9.
[8] LIN C Y, LEE W J, CHEN S J, et al. A study of grid artifacts formation and elimination in computed radiographic images[J]. Journal of Digital Imaging, 2006, 19(4): 351−361. doi: 10.1007/s10278-006-0630-8
[9] TANG H. A new stationary gridline artifact suppression method based on the 2D discrete wavelet transform[J]. Medical Physics, 2015, 42(4): 1721−1729. doi: 10.1118/1.4914861
[10] YU Y. A novel grid regression demodulation method for radiographic grid artifact correction[J]. Medical Physics, 2021, 48(7): 3790−3803. doi: 10.1002/mp.14932
[11] WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600−612. DOI: 1109/TIP.2003.819861.



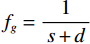
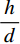

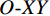
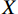
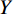
 下载:
下载: