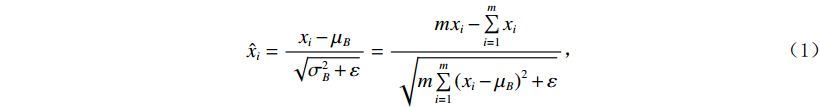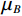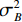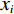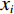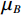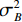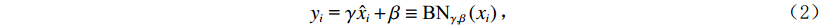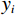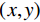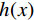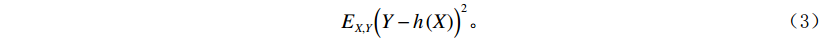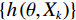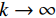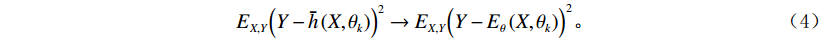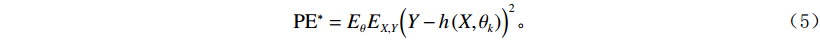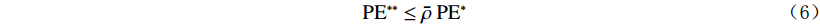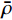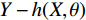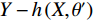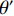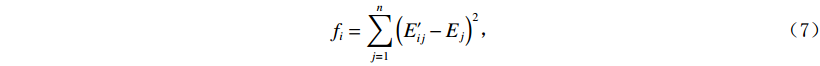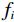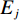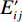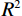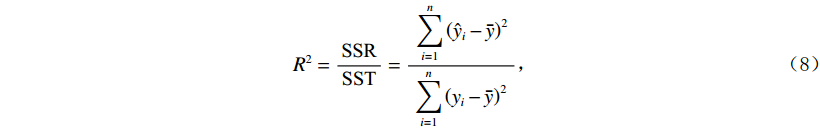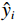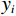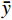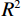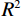Deep Learning Reservoir Parameter Prediction Based on Seismic Attribute Reduction: Take Ledong Area of Yinggehai Basin as an Example
-
摘要: 储层物性参数作为描述储层特性、储层建模和流体模式的重要指标，其准确估算可以为储层预测提供有力参考依据，但传统储层物性参数反演方法无法兼顾反演精度及空间连续性。针对上述问题，本文引入地震属性作为深度学习算法输入，针对地震属性之间存在的信息冗余特征，利用随机森林-递归消除法对地震属性进行约简预处理，最终建立一种基于地震属性约简的储层物性参数预测方法。实际数据测试结果表明，地震属性约简的深度学习储层物性参数预测结果具有良好的精度及横向分辨率，证实本文方法的有效性。Abstract: As an important indicator to describe reservoir characteristics, reservoir modeling and fluid model, the accurate estimation of reservoir physical parameters can provide a powerful reference for reservoir prediction, but the traditional inversion method of reservoir physical parameters can not give consideration to inversion accuracy and spatial continuity. To solve the above problems, this paper introduced seismic attributes as input of deep learning algorithm. Aiming at the information redundancy among seismic attributes, random forest-recursive elimination method was used to reduce the seismic attributes, thus a prediction method of reservoir physical property parameters based on seismic attribute reduction was finally established. The actual data test results showed that the prediction results of reservoir physical parameters by deep learning based on seismic attribute reduction presented good accuracy and lateral resolution, which confirmed the effectiveness of the proposed method.
-
随着国内油气勘探的发展，勘探领域由常规构造油气藏逐步向岩性油气藏等复杂储层转移，勘探目标日趋复杂，勘探难度不断增大，对储层预测技术也提出更高的要求。储层物性参数（孔隙度、泥质含量、含流体饱和度与渗透率等）是描述储层特性、流体模式和储层建模的重要指标，其准确估计能够为储层预测提供有力参考依据。但基于线性假设的常规储层物性参数反演方法已难以满足勘探新局面下的高精度储层描述需求，迫切需要引入新的非线性模型来解决储层物性参数预测问题。
用神经网络指挥非线性反演系统，使之输出分辨率最优而方差最小的地球模型，是下一阶段非线性反演研究的一个重要方向[1]。深度学习技术作为人工智能中发展最快的分支，解决难以形式化的非线性问题是其核心竞争力，其本质是构建含多隐层的运算模型。借助计算机对大规模数据进行迭代计算，深度抽象出更能代表标签特征的信息，并将这些信息保留在权重系数关系中，实现对未知问题进行预测。
20世纪90年代，印兴耀等[2-3]便成功使用BP神经网络实现了实际工区物性参数预测，如今深度学习技术与地球物理领域的结合更是日渐广泛，2018年，Xu等[4]使用卷积神经网络进行初至拾取；孙小东等[5]将深度学习技术用于地震数据去噪；针对储层预测中的非线性和信息冗余问题，桑凯恒等[6]基于模糊粗糙集理论进行机器学习储层预测方法研究；2019年，Wu等[7-8]用卷积神经网络实现断层检测；2019年，安鹏等[9-10]基于循环神经网络利用测井曲线预测孔隙度与岩性识别；2020年，闫星宇等[11]使用深度学习技术实现了地震相智能划分；陈康等[12]在2021年提出了一种改进U-Net卷积神经网络，在岩性识别及甜点预测上取得了较好的应用效果。伴随深度学习与地球物理学的发展与结合，地球物理学领域中深度学习的应用取得了许多突破性进展。
储层物性参数与地震属性都是地下相同地质体的综合反映，两者间必然存在很强的相关关系，但这种关系并非是简单的一一对应关系，也没有定量的数学公式表征[13]。因此将人工智能与储层物性参数反演相结合，使用深度学习技术对地震属性与储层物性参数之间隐含的非线性关系进行映射，进而实现储层物性参数的有效预测。然而目前常用的地震属性种类已多达上百种，众多属性彼此间存在大量的冗余信息[14]，将其全部作为神经网络的输入，计算机承受更大压力的同时，容易使神经网络模型产生过拟合问题。
综上，针对不同的实际工区与地质条件，对地震属性集合进行约简预处理，建立涵盖当前工区地质特征的地震属性子集，是保证反演算法高效稳定的必要手段。
从深度学习的角度，地震属性约简属于特征工程中的特征选择问题。特征选择的方法大致可以分为过滤法（Filter）、包裹法（Wrapper）与嵌入法（Embedding）三大类[15-17]。随机森林算法作为人工智能中另一重要分支，在生产研究中已有较成熟应用，具有算法成熟、调参简洁以及支持并行运算等优势[18-19]。将其应用至地震属性约简可归类于嵌入法，可以根据随机森林的特征权重值系数对每维输入进行重要度排序，并将其与递归消除法结合获得约简属性子集[20]。
本文以储层物性参数预测为目标，以深度学习作为研究方法，辅以地震属性约简方法，对地震属性与储层物性参数间隐含的非线性映射关系进行描述，提出一种基于地震属性约简的深度学习储层物性参数预测方法，用于实际储层描述与刻画。
1. 方法理论
1.1 BN优化深度神经网络
深度神经网络（deep neural networks，DNN）是一种深度学习的基础，相比于针对具有空间结构问题的卷积神经网络（convolutional neural networks，CNN），针对时序问题的循环神经网络（recurrent neural network，RNN），DNN网络结构简洁，在解决无特殊结构问题时更具普适性[21]。
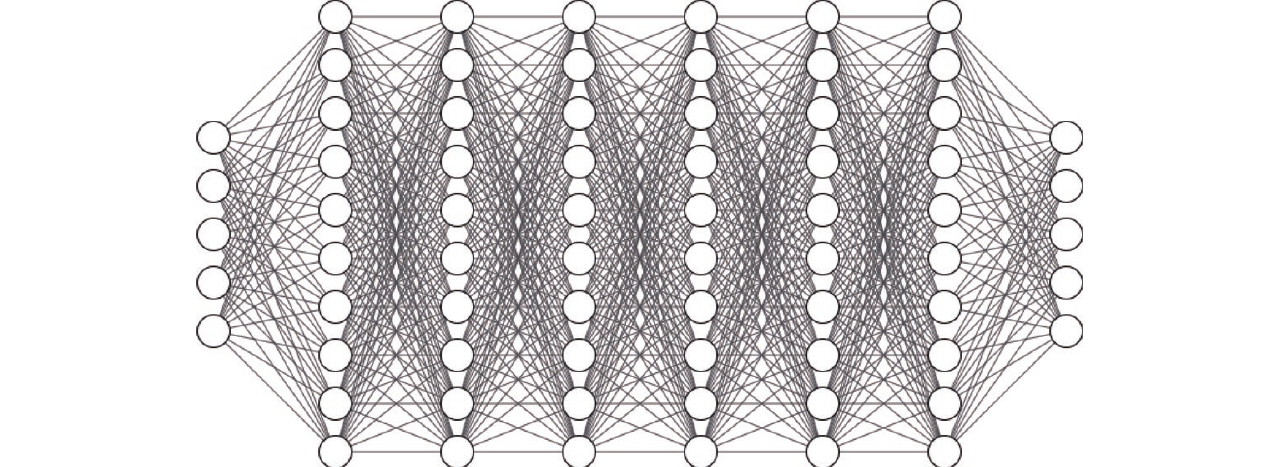
如图1所示，DNN与传统BP神经网络（back propagation neural network，BPNN）具有相同的拓扑结构，除隐藏层层数不同外，两者在结构上是相同的，其作为全连接神经网络从输入层出发，由隐藏层到输出层，层与层之间的神经元相互连接，但层内的神经元不连接。DNN等深度学习技术之所以取得成功，除了比传统浅层神经网络具有更深的隐藏层深度外，更表现在预训练与权重初始化、激活函数以及优化算法等方面。
DNN相对于传统神经网络具有更深的隐层层数、更多的神经元个数以及更复杂的网络结构，因此具备更强的拟合能力以及更高的精度，但同时也带来了过拟合问题，即神经网络模型在训练集上效果较好，而在应用至测试集时效果较差。
为克服过拟合问题以及进一步提高其训练速度与预测精度，本文对DNN模型进行批量标准化（batch normalization，BN）优化处理。在训练神经网络时，往往首先需要对输入层数据标准化以提高训练的速度，而BN的基本思想与之类似，在训练过程中不仅对输入层数据标准化，而且对每个隐层的每批数据都进行标准化处理[22-23]，具体公式：
$$ {\hat x_i} = \frac{{{x_i} - {\mu _B}}}{{\sqrt {\sigma _B^2 + \varepsilon } }} = \frac{{m{x_i} - \sum\limits_{i = 1}^m {{x_i}} }}{{\sqrt {m\sum\limits_{i = 1}^m {{{\left( {{x_i} - {\mu _B}} \right)}^2}} + \varepsilon } }} \text{，} $$ (1) 式中m为每批样本个数，
$ {\mu _B} $ 与$ \sigma _B^2 $ 分别为每批样本$ {x_i} $ 的均值和方差，ε为防止方差为 0产生无效计算引入的极小值。利用公式（1），首先在每个隐层激活函数前计算每批样本
$ {x_i} $ 的均值$ {\mu _B} $ 和方差$ \sigma _B^2 $ ，然后对每批样本数据标准化处理，最后进行变换重构，以恢复原始网络的特征分布：$$ {y_i}{\text{ = }}\gamma {\hat x_i} + \beta \equiv {\text{B}}{{\text{N}}_{\gamma ,\beta }}\left( {{x_i}} \right) \text{，} $$ (2) 式中
$ {y_i} $ 为BN层输出；γ为缩放参数；β为偏移参数。1.2 随机森林算法
随机森林作为一种机器学习算法，在分类、回归等问题均有很成功应用的案例，是一种利用决策树分类器形成的融合算法，其基本原理是利用自助法和重采样方法从初始样本集中随机抽取多个样本，并以每个样本分别构建决策树，最后将随机部分决策树的预测值取平均作为随机森林的预测值。
董师师等[24]给出了随机森林算法基本流程，设随机森林的训练集为独立同分布的随机向量
$ (x,y) $ ，则预测值$ h(x) $ 的均方泛化误差为：$$ {E_{X,Y}}{\Big( {Y - h\left( X \right)} \Big)^2} 。 $$ (3) 则随机森林的总输出是对随机k可决策树的预测值
$ \left\{ {h\left( {\theta ,{X_k}} \right)} \right\} $ 取平均值得到的，当$ k \to \infty $ 时，$$ {E_{X,Y}}{\left( {Y - \bar h\left( {X,{\theta _k}} \right)} \right)^2} \to {E_{X,Y}}{\Big( {Y - {E_\theta }\left( {X,{\theta _k}} \right)} \Big)^2} 。 $$ (4) 将式（4）右边部分为随机森林泛化误差标记为PE**，则每棵决策树的平均泛化误差PE*公式为：
$$ {\rm{P}}{{\rm{E}}^*} = {E_\theta }{E_{X,Y}}{\Big( {Y - h\left( {X,{\theta _k}} \right)} \Big)^2} 。 $$ (5) 对所有θ有：
$$ {\rm{P}}{{\rm{E}}^{**}} \leq \bar \rho \;{\rm{P}}{{\rm{E}}^*} $$ (6) 其中
$ \bar \rho $ 为残差$ Y - h(X,\theta ) $ 和$ Y - h\left( {X,{\theta ^\prime }} \right) $ 的加权相关系数，且θ与$ {\theta ^\prime } $ 相互独立，公式（6）给出了精确回归随机森林的要求。随机森林的评价标准是根据袋外数据误差来进行属性约简的重要度排序，袋内数据是指在训练时每一个决策树抽取到的样本的集合，而袋外数据是计算时没有被抽取到的样本集合，具体的重要性评估公式为：
$$ {f_i} = \sum\limits_{j=1}^n {{{\left( {E_{ij}^\prime - {E_j}} \right)}^2}} \text{，} $$ (7) 其中
$ {f_i} $ 为第i个属性的重要度，$ {E_j} $ 为第j棵决策树使用袋外数据计算的校验误差，$ E_{ij}^\prime $ 为第i个待评估特征第j棵决策树使用随机打乱的袋外数据计算的校验误差。1.3 基于随机森林-递归消除法的属性约简算法
递归消除法是一种处理问题的策略，往往需要与回归模型或者支持向量机等结合作为顶层算法，主要思想是在每次迭代过程中，通过与之相结合的模型算法，利用当前的属性集合构建模型。每轮迭代后消除若干权值系数的属性，再基于新的属性集进行下一轮迭代。遍历所有属性，最后通过交叉验证来找到最优的属性。
随机森林具有上述优势并已广泛应用于分类、回归等问题，但利用随机森林进行地震属性约简时，我们最后得到的是单维属性的排列顺序（按照属性的重要性程度降序排列），无法判断最终属性子集保留维数，需要人工主观判断[25]。基于以上考虑，将递归消除中后向迭代、交叉验证的思想与随机森林相结合，形成随机森林-递归消除法（RF-RFE），进而避免人为因素造成的影响，更加合理的判断约简得到的子集维度。
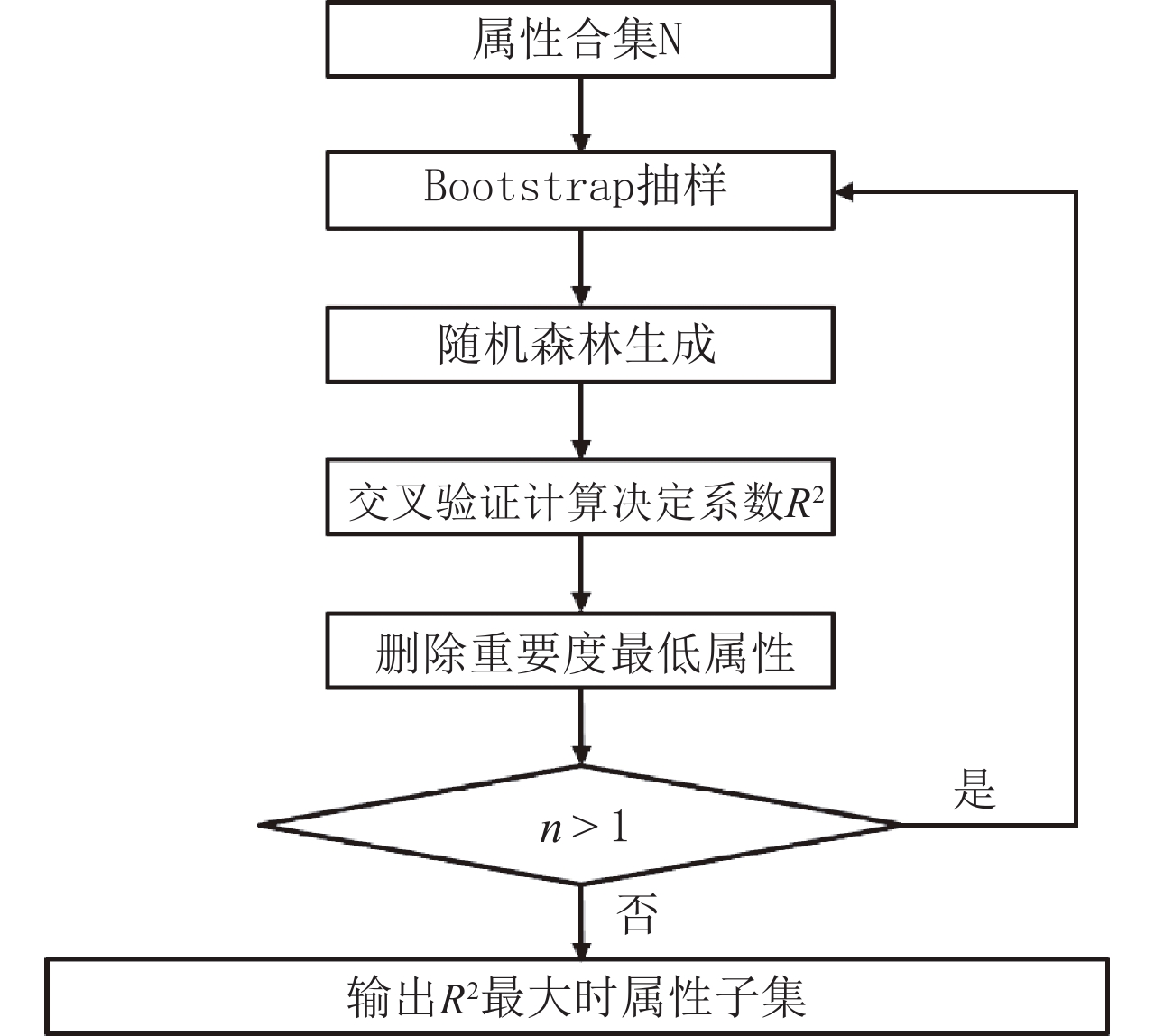
RF-RFE算法用于属性约简的整体流程如图2所示，具体步骤：
（1）假设原始属性合计N的维度为n，使用boosttrap有放回式抽样随机抽取m个样本子集，由此m个样本子集形成m棵回归树再构成随机森林，未被抽取到的数据组成袋外数据。
（2）随机森林生成后，根据公式（7）逐维求取属性重要度，数值越大重要程度越高，进而得到属性重要度排序。
（3）使用10折交叉验证求取回归决定系数
$ {R^2} $ ，公式如下：$$ {R^2} = \frac{{{\text{SSR}}}}{{{\text{SST}}}} = \frac{{{\kern 1pt} \displaystyle\sum\limits_{i = 1}^n {{{\left( {{{\hat y}_i} - \bar y} \right)}^2}{\kern 1pt} } }}{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} }} \text{，} $$ (8) 其中SSR为回归平方和，SST为总离差平方和，n为样本个数，
$ {\hat y_i} $ 为预测值，$ {y_i} $ 为真实值，$ \bar y $ 为真实值均值[26]。（4）按照步骤（2）中获得的重要度排序，将排序最低的属性从属性集移除，重复上述步骤迭代处理，逐步移除重要度最小的属性，直到剩余一个属性，输出结果，选择回归决定系数最大时所对应的特征个数，并按排序结果输出。
2. 实例测试
2.1 基于RF-RFE算法的地震属性约简
地震属性发展至今，用于储层预测的属性种类已多达上百种。在进行储层参数预测过程时，我们往往尽可能多的提取地震属性，是一个“由少到多”的过程。然而，虽然地震属性的增多在一定程度上可以为我们提供更多的地下信息，但与此同时属性的不断增加带给后续计算更大的压力，占据了大量的存储空间的同时，势必会消耗更多的计算时间；其次，在针对某一具体问题时，众多的属性中大多都是冗余的，甚至带来干扰噪声影响；最后，地震属性间存在高相关关系的信息，若未进行属性约简处理，必然会造成信息浪费，同时给神经网络带来过拟合等问题。因此，借助深度学习进行储层物性参数预测前对地震属性约简是必要的，进行一个“由多到少”的地震属性约简过程。
本文以我国近海海域莺歌海盆地某实际工区作为实例测试，该工区包含5口已知井，岩石物理特征变化规律较为复杂，受高温高压、低速泥岩、底辟发育等多种因素共同影响。经岩石物理分析，浅层砂岩呈现低速度、低密度、低阻抗特征，随埋深变化，压实作用增强，砂泥岩阻抗值逐渐接近，无法利用传统线性岩石物理模型建立地震响应特征与储层物性参数间的映射关系，使得常规物性参数反演方法应用效果欠佳。
根据本文方法流程，首先对地震属性进行预处理工作。以实际地震数据作为输入，利用商业软件OpendTect提取包括三瞬属性、能量属性及统计属性等常规地震属性40种，以具体反演目标选择不同的测井曲线作为约简标签。以孔隙度反演为例，将重采样等预处理后的孔隙度曲线作为约简标签，使用RF-RFE算法对提取的40种地震属性进行属性约简。
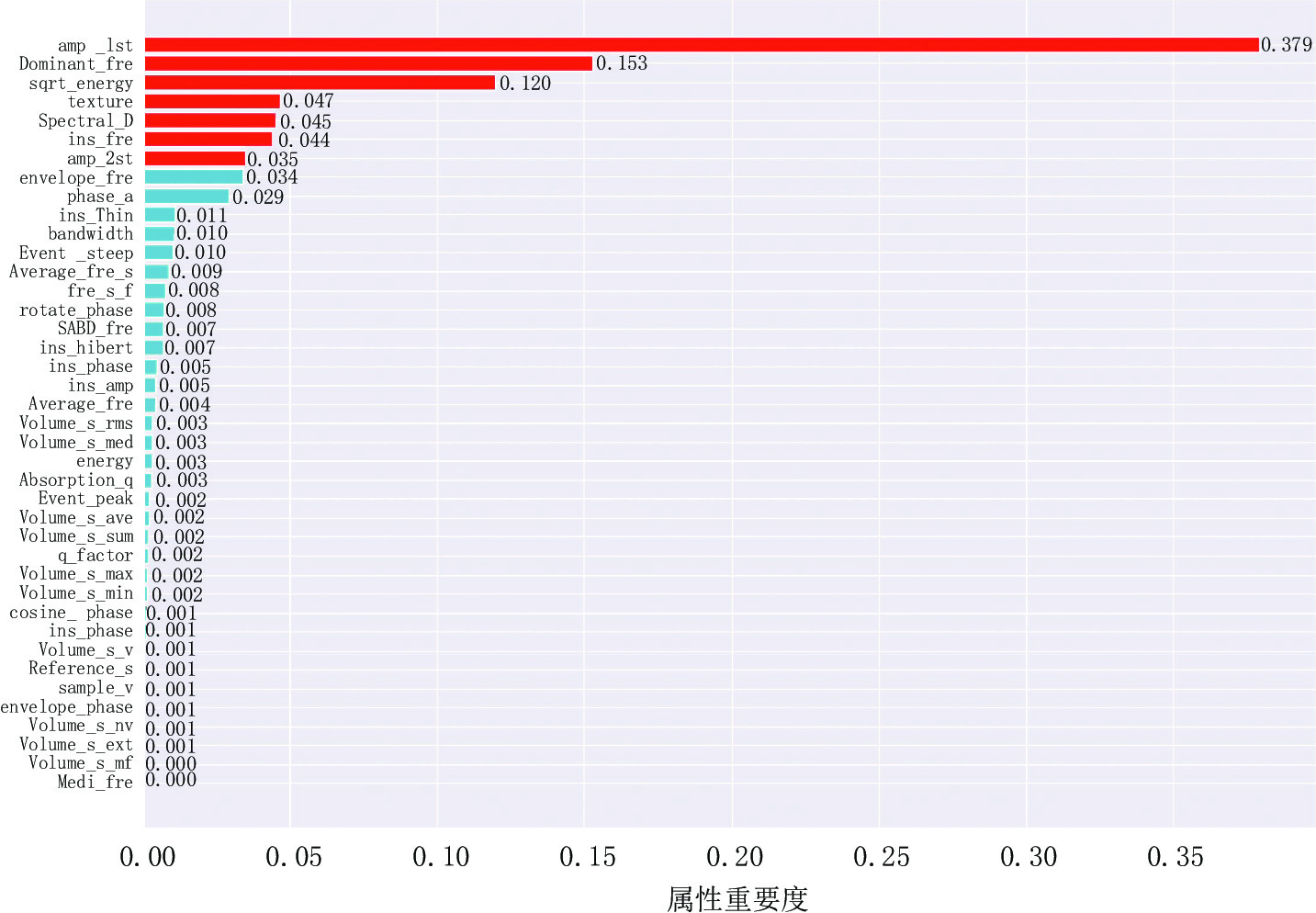
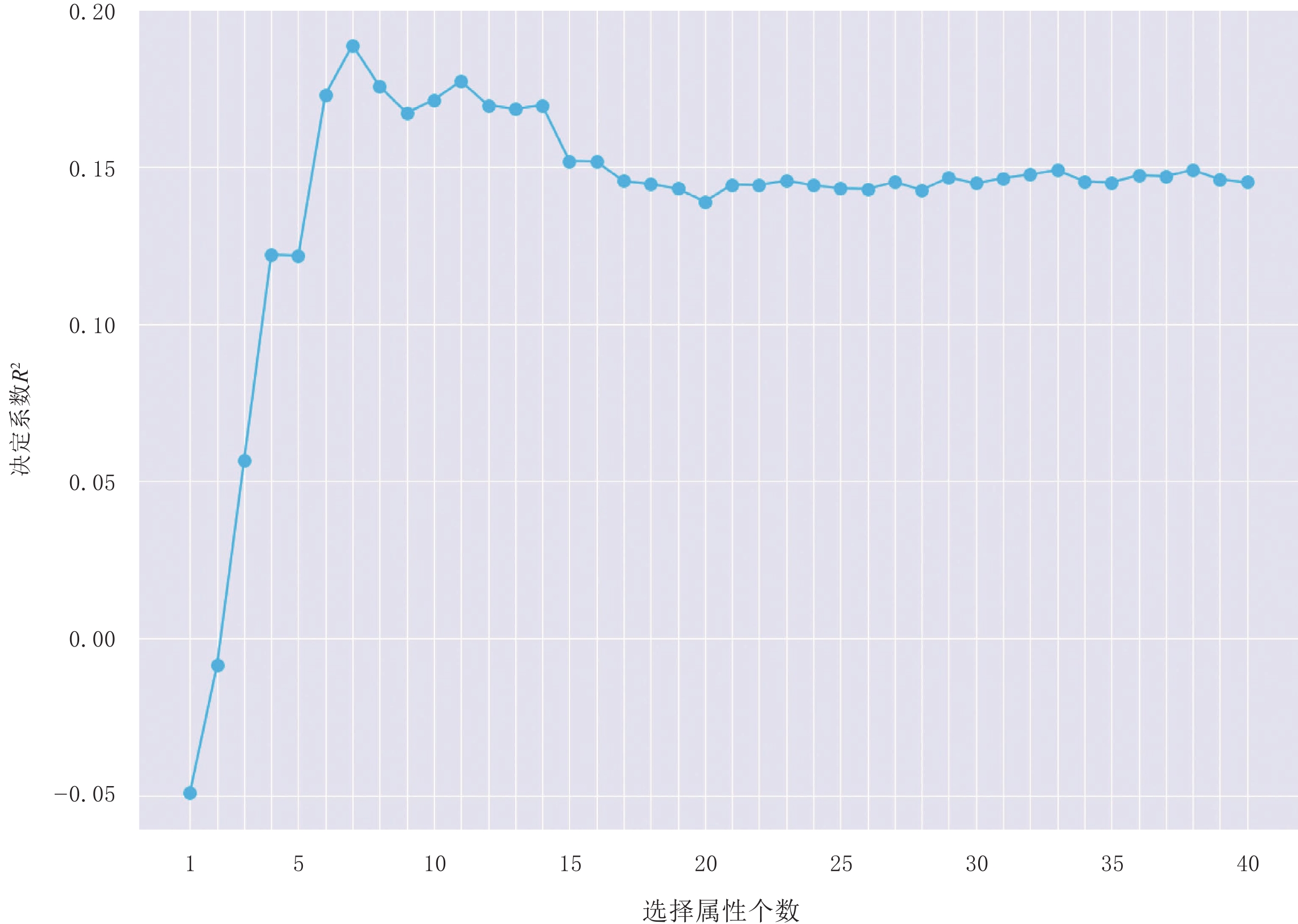
首先，对地震属性进行标准化处理，与约简标签孔隙度曲线构成样本数据，使用boosttrap有放回式抽样后生成随机森林，根据公式（7）求取地震属性的重要度，得到属性重要度排序（图3）。然后，利用递归消除后向迭代法，逐步消除重要度排序中重要的最低的属性，并通过交叉验证的思想，根据公式（8）对每次迭代后的模型求取决定系数（图4）。最后，结合决定系数分析，确定地震属性个数。如图4所示，对于实验工区地震属性特征，属性个数为7的时候决定系数达到最大值，即地震属性重要度排序中的前7种地震属性已基本涵盖该工区地下地质体信息特征，对应属性冗余信息最小，预测结果最为精准，能够有效避免后续算法的过拟合问题。因此，针对本工区特征，保留地震属性重要度排序图中的前7种地震属性构建数据集，作为后续深度学习的输入。
![]()
图 4 决定系数随地震属性个数变化图Figure 4. Coefficient of determination varies with the number of seismic attributes2.2 深度学习孔隙度预测方法
以属性约简后得到的7种地震属性作为神经网络输入，以2 ms采样率进行重采样处理的孔隙度曲线作为期望输出，选用的神经网络模型仍为前文构建的BN优化DNN模型，其中隐层层数为8层，每个隐层神经元个数均在50到70个，激励函数采用Relu函数，神经网络优化算法采用Adam算法。
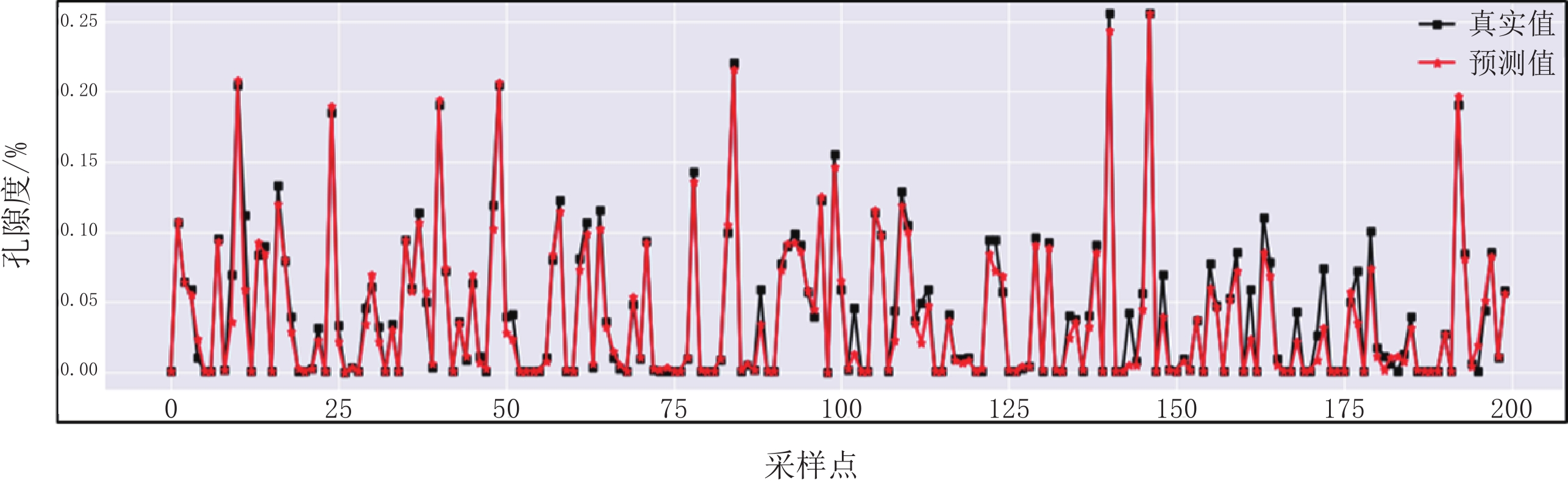
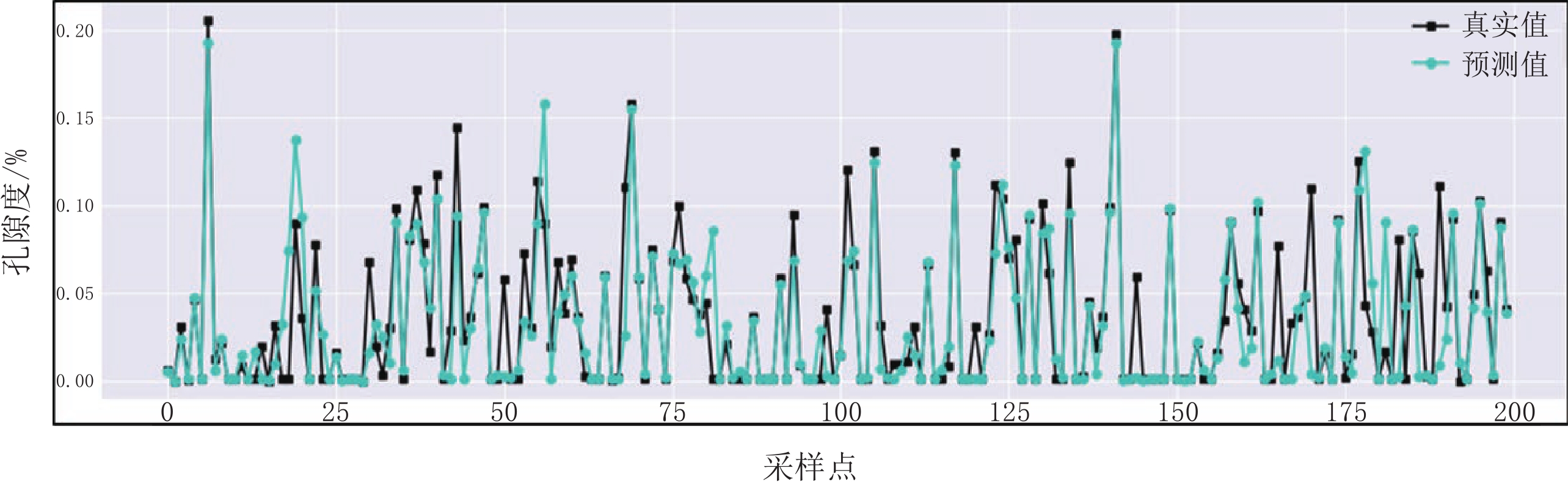
训练集样本个数为1708，测试集样本个数为732，学习率为0.001，经过100000次迭代模型得到了较好的训练，经计算得到在训练集中均方误差（RMSE）为4.792，决定系数
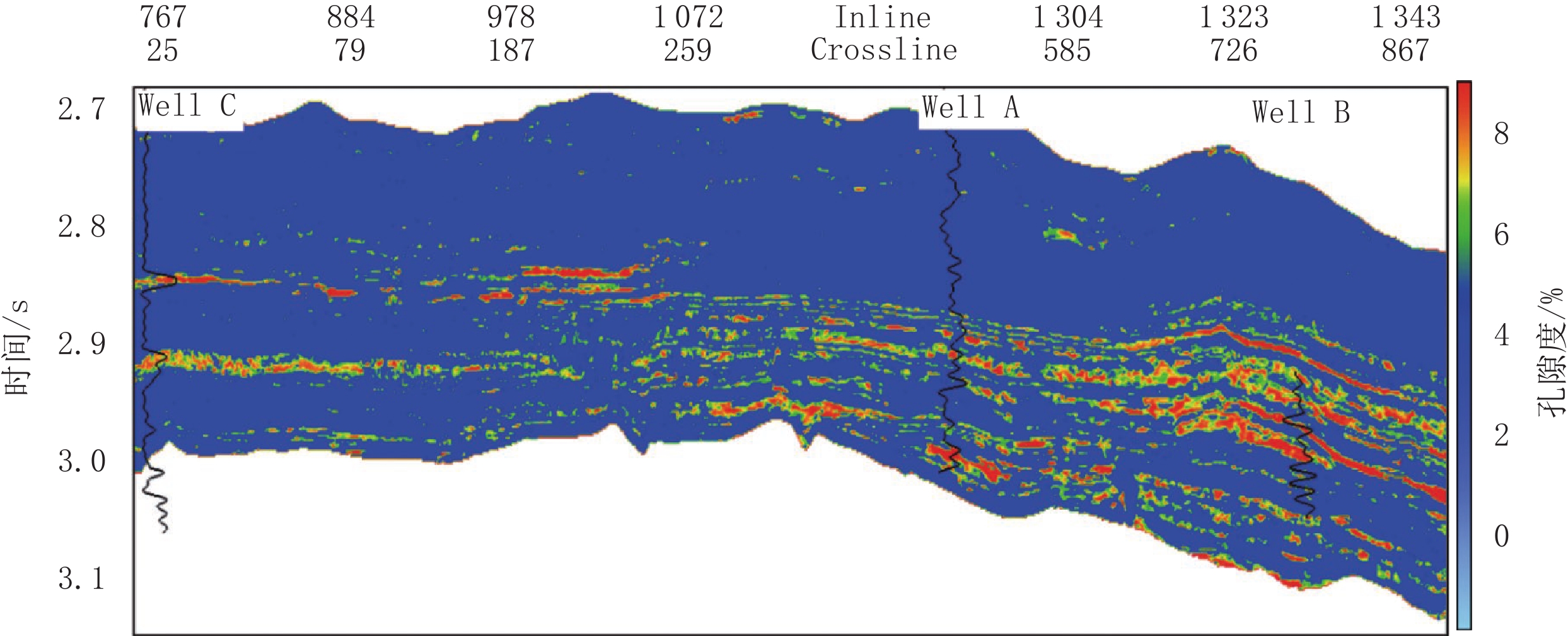
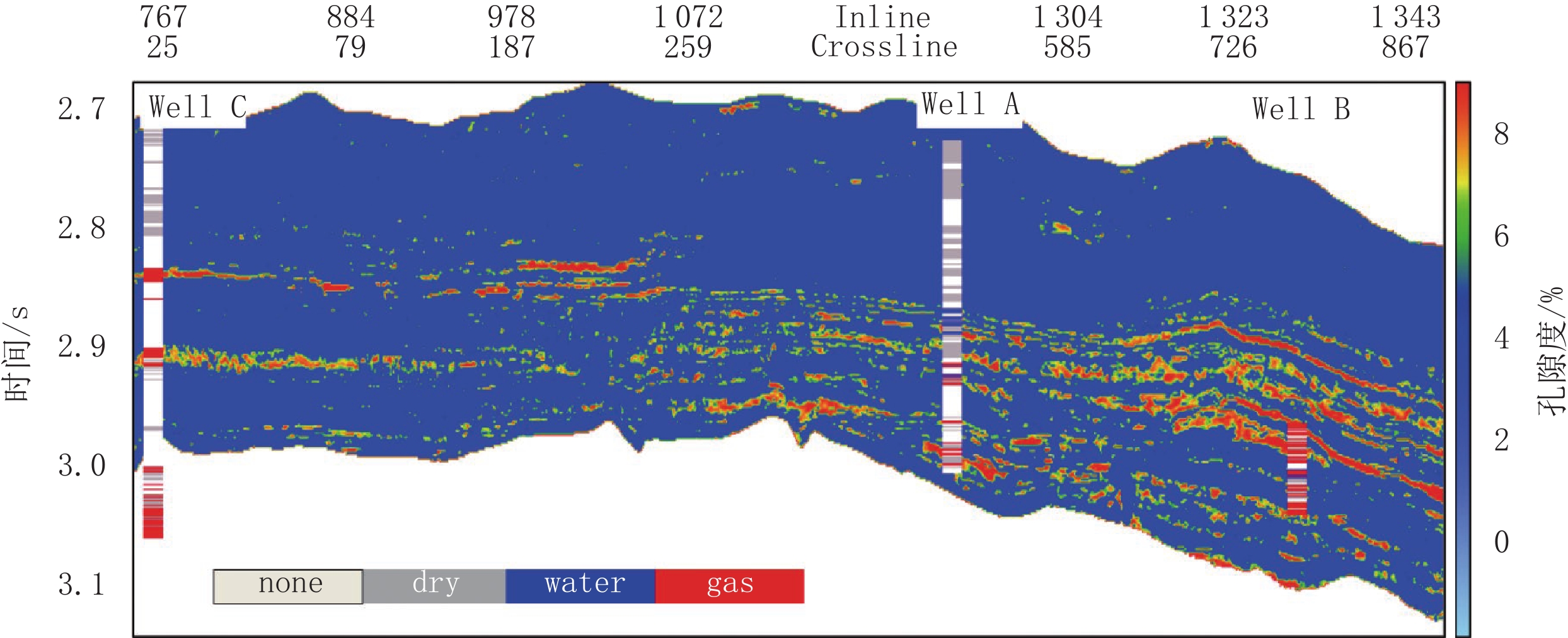
$ {R^2} $ 为0.960；在测试集中均方误差（RMSE）为11.034，决定系数$ {R^2} $ 为0.852。孔隙度实际测井重采样曲线与反演结果在训练集与测试集前200个采样点的对比，如图5和图6所示。![]()
图 5 训练集孔隙度真实值与预测值对比Figure 5. Contrast the actual and predicted values of the porosity curve in train set![]()
图 6 测试集孔隙度真实值与预测值对比Figure 6. Contrast the actual and predicted values of the porosity curve in test set将训练好的模型应用至实际工区过井线剖面，获得孔隙度曲线预测结果的二维展布，如图7和图8所示。由图可知，深度学习孔隙度反演结果与测井孔隙度曲线总体吻合度较高，能够较为精细的刻画储层参数分布情况，但该工区岩石物理特征规律复杂、区域测井资料较少，进而导致个别区域孔隙度与地震属性非线性映射关系较差。孔隙度反演结果与测井含油气性解释结果基本保持一致，根据实际工区岩石物理情况，油气解释气层位置对应实际孔隙度高值，预测孔隙度结果兼具精度与横向分辨率，且符合工区岩石物理特征，证明本文方法的有效性，满足一定的实际生产要求。
![]()
图 8 含油气性测井解释结果与孔隙度反演剖面Figure 8. Oil and gas logging interpretation and porosity inversion profile3. 结论
针对储层物性参数反演存在的信息冗余与非线性问题，本文提出基于随机森林-递归消除法的地震属性约简技术，并基于深度学习进行储层物性参数预测方法研究，结果表明：①使用基于随机森林-递归消除法的地震属性约简方法，可以有效的消除除掉冗余信息，提高储层参数预测精度且节约计算空间与成本。②将深度学习应用至储层物性参数预测，可以有效地解决地震属性与储层参数之间的非线性映射问题，实现储层参数的有效高效预测。
本文的不足之处，本文的方法较依赖于样本数量，在缺井或少井区域反演效果不甚理想，需进行深入的相关研究。
-
![]()
图 4 决定系数随地震属性个数变化图
Figure 4. Coefficient of determination varies with the number of seismic attributes
![]()
图 5 训练集孔隙度真实值与预测值对比
Figure 5. Contrast the actual and predicted values of the porosity curve in train set
![]()
图 6 测试集孔隙度真实值与预测值对比
Figure 6. Contrast the actual and predicted values of the porosity curve in test set
-
[1] 杨文采. 神经网络算法在地球物理反演中的应用[J]. 石油物探, 1995,34(2): 116−120. YANG W C. Application of neural network alogorithms to geophysical inversion[J]. Geophysical Prospecting for Petroleum, 1995, 34(2): 116−120. (in Chinese).
[2] 印兴耀, 吴国忱, 张洪宙. 神经网络在储层横向预测中的应用[J]. 石油大学学报(自然科学版), 1994,18(5): 20−26. YIN X Y, WU G C, ZHANG H Z. The application of neural networks in the reservior prediction[J]. Journal of China University of Petroleum (Edition of Natural Science), 1994, 18(5): 20−26. (in Chinese).
[3] 印兴耀, 杨风丽, 吴国忱. 神经网络在CB油田储层预测和储层厚度计算中的应用[J]. 石油大学学报(自然科学版), 1998,22(2): 3−5. YIN X Y, YANG F L, WU G C. Application of neural network to predicting reservoir and calculating thickness in CB oilfield[J]. Journal of China University of Petroleum (Edition of Natural Science), 1998, 22(2): 3−5. (in Chinese).
[4] XU Y, YIN C, PAN Y, et al. First-break automatic picking technology based on semantic segmentation[J]. Geophysical Prospecting, 2021, 69(6): 1181-1207.
[5] 孙小东, 王伟奇, 任丽娟, 等. 地震数据智能去噪与传统去噪方法的对比及展望[J]. 地球物理学进展, 2022, 35(6): 2211-2219. SUN X D, WANG W Q, REN L J, et al. Comparison and prospect on AI denoising of seismic data along with traditional denoising methods[J]. Progress in Geophysics, 2020, 35(6): 2211-2219. (in Chinese).
[6] 桑凯恒, 张繁昌. 基于模糊粗糙集的机器学习储层参数预测[J]. CT理论与应用研究, 2018,27(4): 455−464. DOI: 10.15953/j.1004-4140.2018.27.04.05. SANG K H, ZHANG F C. Prediction of reservoir parameters of machine learning based on fuzzy rough set[J]. CT Theory and Applications, 2018, 27(4): 455−464. DOI: 10.15953/j.1004-4140.2018.27.04.05. (in Chinese).
[7] WU X, LIANG L, SHI Y, et al. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35−IM45. doi: 10.1190/geo2018-0646.1
[8] WU X, YAN S, QI J, et al. Deep learning for characterizing paleokarst collapse features in 3D seismic images[J]. Journal of Geophysical Research: Solid Earth, 2020.
[9] 安鹏, 曹丹平, 赵宝银, 等. 基于LSTM循环神经网络的储层物性参数预测方法研究[J]. 地球物理学进展, 2019, 34(5): 1849-1858. AN P, CAO D P, ZHAO B Y, et al. Reservoir physical parameters prediction based on LSTM recurrent neural network[J]. Progress in Geophysics, 2019, 34(5): 1849-1858. (in Chinese).
[10] 安鹏, 曹丹平. 基于深度学习的测井岩性识别方法研究与应用[J]. 地球物理学进展, 2018,33(3): 1029−1034. doi: 10.6038/pg2018BB0319 AN P, CAO D P. Research and application of logging lithology identification based on deep learning[J]. Progress in Geophysics, 2018, 33(3): 1029−1034. (in Chinese). doi: 10.6038/pg2018BB0319
[11] 闫星宇, 顾汉明, 罗红梅, 等. 基于改进深度学习方法的地震相智能识别[J]. 石油地球物理勘探, 2020,55(6): 1169−1177. YAN X Y, GU H M, LUO H M, et al. Intelligent seismic facies classification based on an improved deep learning method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1169−1177. (in Chinese).
[12] 陈康, 狄贵东, 张佳佳, 等. 基于改进U-Net卷积神经网络的储层预测[J]. CT理论与应用研究, 2021,30(4): 403−416. DOI: 10.15953/j.1004-4140.2021.30.04.01. CHEN K, DI G D, ZHANG J J, et al. Reservoir prediction based on improved U-Net convolutional neural network[J]. CT Theory and Applications, 2021, 30(4): 403−416. DOI: 10.15953/j.1004-4140.2021.30.04.01. (in Chinese).
[13] PURVES S, ALAEI B, BONAS J B, et al. Machine learning from core to seismic; Porosity prediction in the Norwegian North Sea[C]//81st EAGE Conference and Exhibition 2019. European Association of Geoscientists & Engineers, 2019, 2019(1): 1-5.
[14] 印兴耀, 周静毅. 地震属性优化方法综述[J]. 石油地球物理勘探, 2005,40(4): 482−489. doi: 10.3321/j.issn:1000-7210.2005.04.027 YIN X Y, ZHOU J Y. Summary of optimum methods of seismic attributes[J]. Oil Geophysical Prospecting, 2005, 40(4): 482−489. (in Chinese). doi: 10.3321/j.issn:1000-7210.2005.04.027
[15] 郭淑文, 程然, 祝文亮, 等. 数据挖掘技术在地震属性降维中的应用[J]. 天然气地球科学, 2010,21(4): 670−677. GUO S W, CHENG R, ZHU W L, et al. Application of data mining technique in reduction of dimensions of seismic attribute parameters[J]. Natural Gas Geoscience, 2010, 21(4): 670−677. (in Chinese).
[16] ROWEIS S, SAUL L. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323−2326. doi: 10.1126/science.290.5500.2323
[17] CHEN Q, SIDNEY S. Advances in seismic attribute technology[J]. Seg Technical Program Expanded Abstracts, 1949, 16(1): 2067.
[18] 王全才. 随机森林特征选择[D]. 大连: 大连理工大学, 2011. WANG Q C. Random forest feature selection[D]. Dalian: Dalian University of Technology, 2011. (in Chinese).
[19] 姚登举, 杨静, 詹晓娟. 基于随机森林的特征选择算法[J]. 吉林大学学报(工学版), 2014(1): 142-146. YAO D J, YANG J, ZHAN X J. Feature selection algorithm based on random forest[J]. Journal of Jilin University (Engineering and Technology Edition), 2014(1): 142-146. (in Chinese).
[20] 宁永鹏. 高维小样本数据的特征选择研究及其稳定性分析[D]. 厦门: 厦门大学, 2014. NING Y P. Study on feature selection and stability analysis of high dimensional small sample data[D]. Xiamen: Xiamen University, 2014.
[21] XIE S, GIRSHICK R, DOLLÁR P, et al. Aggregated residual transformations for deep neural networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017: 1492-1500.
[22] SHIRO T, YUKI Y, MASATO O. Impact of layer normalization on single-layer perceptron: Statistical mechanical analysis[J]. Journal of the Physical Society of Japan, 2019, 88(7).
[23] SHOUJI S, SHIGEKO S I, YOUICHI K. Normalization processes an topographic mapping model between cell layers represented by undirected graphs[J]. Journal of Japan Society for Fuzzy Theory and Systems, 2017, 14(1): 43-54.
[24] 董师师, 黄哲学. 随机森林理论浅析[J]. 集成技术, 2013,2(1): 1−7. doi: 10.5121/ijite.2013.2101 HUANG S S, HUANG Z X. A brief theoretical overview of random forests[J]. Journal of Integration Technology, 2013, 2(1): 1−7. (in Chinese). doi: 10.5121/ijite.2013.2101
[25] 周雪晴, 张占松, 张超谟, 等. 基于粗糙集-随机森林算法的复杂岩性识别[J]. 大庆石油地质与开发, 2017,(6): 131−137. ZHOU X Q, ZHANG Z S, ZHANG C M. et al. Complex lithologic iidentification based on rough set-random forest algorism[J]. Petroleum Geology & Oilfield Development in Daqing, 2017, (6): 131−137. (in Chinese).
[26] 胥雪炎, 李补喜. 不同被解释变量选择对决定系数R2的影响研究[J]. 太原科技大学学报, 2007,28(5): 363−365. XU X Y, LI B X. Research on the effect of selection of dependent variables on R2 statistic[J]. Journal of Taiyuan University of Science and Technology, 2007, 28(5): 363−365. (in Chinese).
-
期刊类型引用(1)
1. 刘军，钟洁，倪振，王庆国，冯仁蔚，贾将，梁岳立. 基于机器学习的低含油饱和度砂岩储层参数预测——以准噶尔盆地夏子街油田夏77井区下克拉玛依组为例. 石油实验地质. 2024(05): 1123-1134 . 
百度学术
其他类型引用(4)
下载:
计量
- 文章访问数: 395
- HTML全文浏览量: 97
- PDF下载量: 57
- 被引次数: 5
